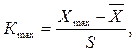
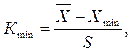Машиностроение \ Метрология, стандартизация и сертификация

Метрология, стандартизация, сертификация. Нормирование точности: Лабораторный практикум, страница 10

                                                      (2)

где S – среднее квадратичное отклонение отдельного наблюдения от x

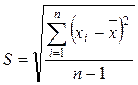
Затем находят теоретическое значение параметра Кp в зависимости от n и доверительной вероятности Р по таблице 2.

Таблица 2

n

Кр

P = 0,9

P = 0,95

P = 0,99

5

6

7

8

9

10

1,79

1,89

1,97

2,04

2,10

2,15

1,87

2,00

2,09

2,17

2,24

2,29

1,96

2,13

2,26

2,37

2,46

2,54

Если Кmax  > Кр  или Кmin > Кp, то измерение следует считать грубым и отбросить.

После оценки доброкачественности измерений определяют случайную составляющую погрешности измерений Δизм.сл

,

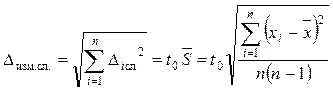где  – среднее квадратичное отклонение  от А (ошибка измерения).

Если , то случайной погрешностью измерений по сравнению с систематической пренебрегают.

При симметричной погрешности результаты измерений представляют в виде:

A ± Δизм.сл., Р.

В общем случае A, Δ от ΔH до ΔB, P (ΔH, ΔB – соответственно нижняя и верхняя границы погрешности измерения Δ).

Пример. В производственных условиях произведены четыре измерения диаметра вала микрометром нулевого класса (микрометр не аттестован, условия измерений соответствуют ГОСТ 8.050-73).

Показания записаны в таблицу 3.

Таблица 3

Номер измерения

Показания X, мм

, мм

, мм2

1

7,97

-0,001

1∙10-6

2

7,975

+0,004

16∙10-6

3

7,965

-0,006

36∙10-6

4

7,974

+0,003

9∙10-6

Среднее арифметическое значение измерений  = 7,971 мм. Систематическая составляющая погрешности измерения (учтенная) равна нулю. Случайная составляющая погрешности измерения

,

по таблице 1 для n = 4, n – 1 = 3 (число степеней свободы) и P = 0,95, t0 = 3,182

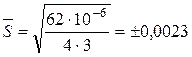 мм.

Так как в данном случае микрометр не аттестован, а известен лишь его класс, систематическая погрешность измерения переходит в разряд случайных и должна быть учтена по известному пределу допускаемой погрешности средства измерения  мм.

 мм.

Измеренный диаметр вала d = 7,971 ± 0,008 мм, P = 0,95.

Оборудование и инструмент: микрометр первого класса с ценой деления 0,01 мм, набор деталей.

Задание к п. 3.1:

Определить MX и выполнить поверку для микрометрического средства измерения.

Порядок выполнения работы:

3.1. Поверка микрометра гладкого (МК)

3.1.1. Определение погрешности эталона.

Для поверки МК используется эталон более высокого разряда. Для выбора эталона определяется величина его погрешности. Если поправка на точность эталона не вводится, то соотношение погрешностей эталона СИэ и поверяемого МК составляет 1:5.

Для микрометров 1 класса точности ΔСИ ±0,004; ΔИЗМ ±0,007. Для эталона погрешность должна составлять ΔСИ = ΔИЗМ = ± 0,0005 (±0,5мкм). С такой погрешностью изготавливаются концевые меры 3 класса точности.

3.1.2. Из набора концевых мер выбрать 1 меру (т.к. при большем количестве следует произвести суммирование погрешностей концевых мер по правилу

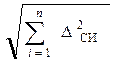
3.1.3. Произвести замер, данные занести в таблицу.

3.1.4. Определить абсолютную ошибку СИ как разность между показаниями СИ(х) и эталона (хд), данные занести в таблицу:

Примечание: в таблице указать знак погрешности

3.1.5. Сделать вывод о пригодности СИ к эксплуатации.

3.1.6. Сделать вывод: каким методом поверки пользовались при аттестации МК.

К п. 3.2:

3.2. Изучить методические указания.

3.3. Измерить деталь микрометром. Провести не меньше 5 замеров в одной точке.

3.4. Определит среднее значение измерения .

3.5. Определить отклонение результатов замеров от среднего значения и занести в таблицу.

Номер измерения

Показания X, мм

, мм

, мм2

3.6. Проверить результаты измерений на отсутствие грубых ошибок. При их наличии измерение считать грубым и отбросить.

3.7. Определить среднее квадратичное отклонение по формуле: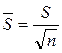

3.8. Определить случайную составляющую погрешности измерения для Р = 0,95 по формуле:   .

Скачать файл