Линейные стационарные цепи. Нелинейные цепи. Параметрические цепи, страница 39

Рассмотрим примеры простейших четырёхполюсников:

Четырёхполюсники первого порядка:

1)

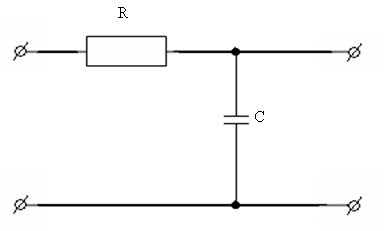
2)

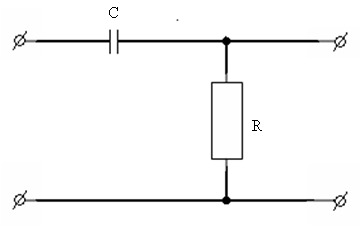
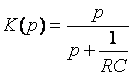
ЧП второго порядка

1)

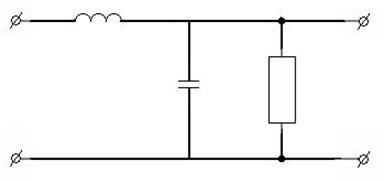
2)

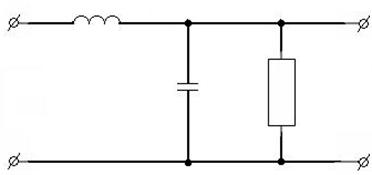
Цепи второго порядка могут быть и безынерционными.

ФНЧ (активная цепь):

7.3  Синтез фильтров

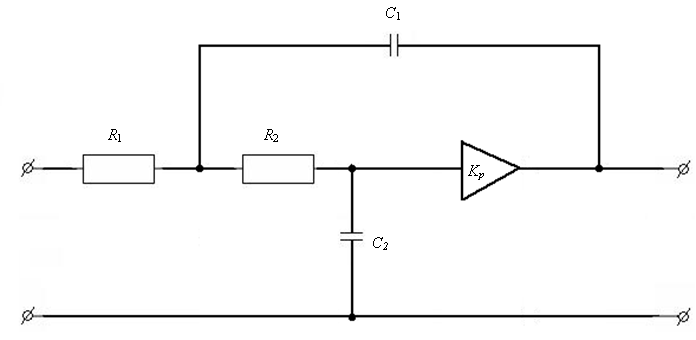
При синтезе фильтров обычно не предъявляют особых требований ФЧХ и в качестве исходных данных для синтеза используют АЧХ, предполагая, что у минимально-фазового ЧП ФЧХ однозначно связано с АЧХ.

Рассмотрим синтез фильтров на примере ФНЧ.

Нормированная характеристика идеального ФНЧ имеет следующий вид:

где

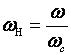
Такая характеристика заведомо не реализуема, поэтому при синтезе используют аппроксимированные АЧХ, при этом аппроксимирующую функцию обычно задают в следующем виде:

Функция F(ω_н) должна быть минимальна по модулю, если ω_н < 1, и максимальна, если ω_н > 1. На практике широко используют фильтры с максимально плоской аппроксимацией и чебышевской аппроксимацией.

Фильтры с максимально плоской аппроксимацией.

В качестве аппроксимирующей функции берётся функция Баттерворда

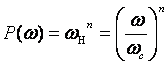
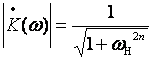
n – порядок фильтра.

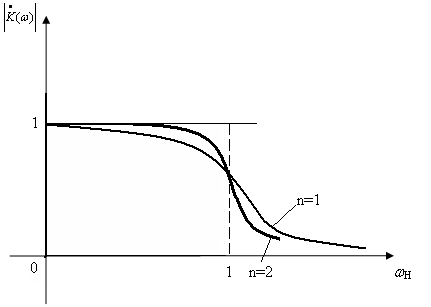
Вне полосы пропускания, когда ω_н >> 1,

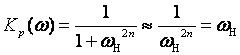
Если это выразить в дБ:

, дБ

Если частоту увеличить в два раза, то ослабление возрастает

-20n·ln2 ≈ 20n·0,3 ≈ -6n дБ/октава

Если частоту увеличить в 10 раз, то затухание будет -20n дБ/октава

Для синтеза структуры фильтра необходимо от частотного коэффициента передачи мощности перейти к коэффициенту передачи мощности на плоскости комплексной частоты. Для этого, тогда:

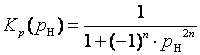
p_н – нормированный оператор Лапласа

Для нахождения полюсов, решим уравнение:

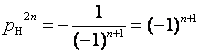
Все корни этого уравнения лежат на окружности единичного радиуса с центром в начале координат, число корней равно 2n, при произвольном n справедливы следующие правила:

1.  Все корни распределены на окрестности равномерно, угловое расстояние между корнями равно .

2.  Если n – нечетное, то первый корень равен единице.

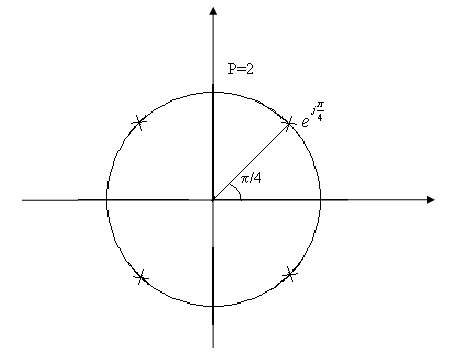
Если n – четное, то первый корень равен .

библиографический список

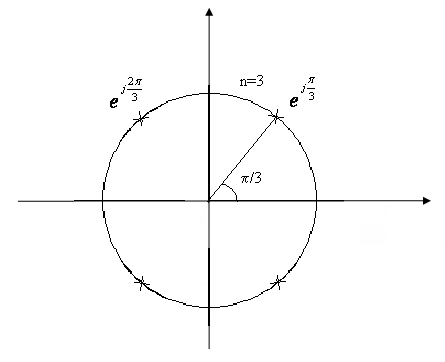
ОСНОВНАЯ