Линейные стационарные цепи. Нелинейные цепи. Параметрические цепи, страница 22

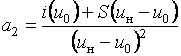
2.  Первый режим большого сигнала

 

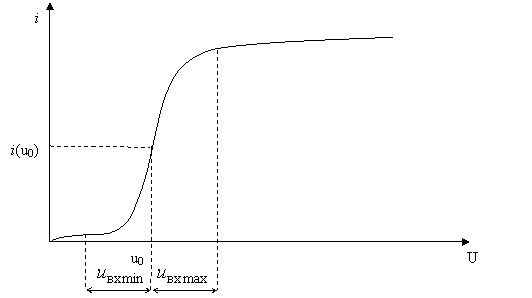
Рис. 5.5 Характеристика БНЭ с рабочей точкой в середине

Рабочая точка находится в точке перегиба, а входное напряжение велико, но не выходит в зоны отсечки и насыщения.

Для аппроксимации в данном случае обычно используют полином третей степени. Учитывая, что в точке перегиба все производные чётного порядка равны нулю, характеристику можно представить в виде:

        

Коэффициент а₁ берут равным крутизне характеристики, т. е. а₁ = S. Коэффициент а₃ обычно определяют из условия, что при                                производная равняется нулю

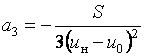
3.  Второй режим большого сигнала

 

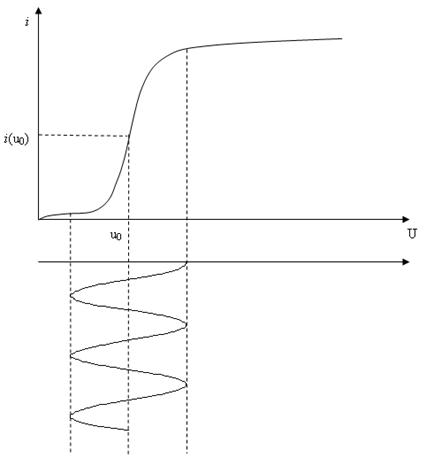Рис. 5.6 Характеристика БНЭ с рабочей точкой в начале

Рабочая точка находится на начальном участке характеристики, а входной сигнал достаточно большой (захватывается зона отсечки).

Для удовлетворительной аппроксимации требуется полином выше пятой степени, практически это нецелесообразно. Более рационально в этом случае использовать кусочно – линейную аппроксимацию. Характеристика при кусочно – линейной аппроксимации заменяется отрезками прямых. Число отрезков может быть любым, однако при большом числе отрезков преимущество её исчезает.

5.1.2  Кусочно-линейная аппроксимация.

Состоит в замене отдельных участков ВАХ нелинейного элемента отрезками прямой линии с различными наклонами. Аналитически ВАХ представляется на каждом отдельном участке.

Аппроксимация определяется двумя параметрами: напряжением начала характеристики U_н и крутизной S, имеющей размерность проводимости. Математическая форма аппроксимированной ВАХ такова:

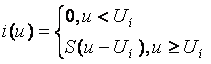
Такую аппрокси­мацию обычно при­меняют при расче­те процессов в не­линейных элемен­тах в случае боль­ших амплитуд внешних воздейст­вий.

5.1.3  Показательная аппроксимация

Для аппроксимации ВАХ диода в области положительных напряжений используют следующее выражение:

I₀ – это обратный ток насыщения, который составляет величину порядка nA или нА.

U_т – температурный потенциал

Для кремниевых диодов при Т = 290 К, u_т = 25 mВ.

Такая аппроксимация характеристики диода допустима при токах, не превышающих нескольких мА, т. е. используется при аппроксимации начального участка.

При больших токах существенным становится объёмное сопротивление проводника и характеристика переходит в линейную.

5.2  Воздействие гармонического сигнала на нелинейные элементы

5.2.1  Воздействие гармонического сигнала при степенной аппроксимации

ВАХ нелинейного элемента описывается степенным полиномом. В этом случае:

i = а₀ + а₁ (и - U₀) + а₂ (и - U₀)² + ...