Линейные стационарные цепи. Нелинейные цепи. Параметрические цепи, страница 31

Рассмотрим методику определения закона распределения сигнала на выходе нелинейного элемента в случае, когда известны закон распределения входного сигнала и функциональная связь между выходным и входным сигналом.

Дано:

y = f(x), P_вх(x)

Определить: P_вых(y)

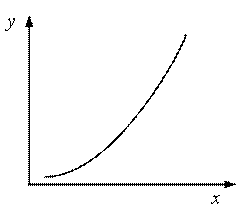
Тогда вероятность попадания входного сигнала на интервал (х; х + dx) будет равна вероятности попадания выходного сигнала на интервал (y; y + dy)

Если функциональная зависимость y = f(x) – убывающая, то 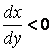, а плотности вероятности отрицательная быть не может, поэтому производную берут по модулю. Если обратная функция является неоднозначной, то обратная функция :

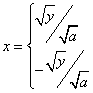
В этом случае находится плотность вероятности для каждой ветви обратной функции, а затем результаты суммируются:

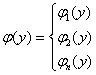
Если на некотором интервале изменение входного сигнала является постоянным, то выходная плотность вероятности будет совершать d-функцию отличную от нуля при значении равном значению выходного сигнала, а площадь под этой d-функцией определяется вероятностью попадания входного сигнала на рассматриваемый интервал:

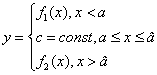
где

Необходимо учитывать условие калибровки:

Пример

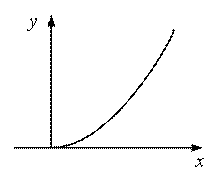
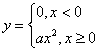
На выходе:

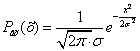
1.

2.

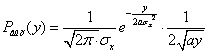y ≥ 0

6  Параметрические цепи

Электрические цепи в которых хотя бы один из параметров изменяется по заданному закону во времени называется цепью с переменными параметрами или параметрической цепью.

Рассмотрим линейный параметрический резистивный элемент и параметрический ёмкостной элемент.