Линейные стационарные цепи. Нелинейные цепи. Параметрические цепи, страница 29

Сигнал на входе частотного детектора можно представить в виде:

(5.1)

 – функция, характеризующая угловую модуляцию.

На выходе частотного детектора:

(5.2)

Для выделения сообщения из частотно-модулированного колебания использование нелинейного недостаточно, т.к. спектр ЧМ сигнала на выходе нелинейного элемента не содержит составляющих, характеризующих сообщение. Требуется дополнительное преобразование. Например, частотный детектор может быть построен по следующей схеме:

Суть преобразования ЧМ колебания в АМ колебание заключаются в следующем: на вход резонансного усилителя подается ЧМ сигнал, причем несущая частота f_o не совпадает с резонансной частотой. Работа ведется на спаде АЧХ.

В это случае K_УС зависит от мгновенной частоты и происходит преобразование ЧМ в АМ. Такой преобразователь возможен, но мало практичен, поскольку контур не настроен на частоту , а АЧХ контура не очень линейна.

На практике широко используют схему двухконтурного детектора:

 

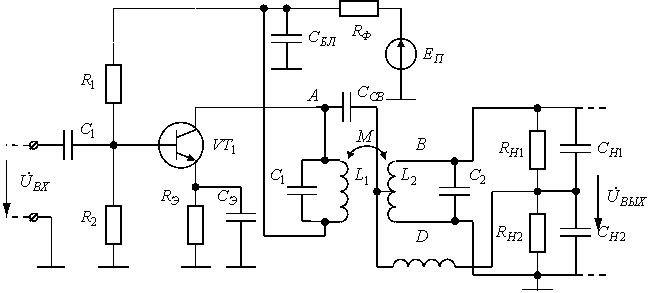
Рис. 5.2 Схема частотного детектора

Рассмотрим случай, когда модуляция отсутствует и на вход детектора поступают гармонические колебания с частотой детектора. Переменный ток, протекающий через катушку индуктивности  наводит на катушке второго контура ЭДС:

(5.3)

Ток во втором контуре в результате действия ЭДС:

(5.4)

где 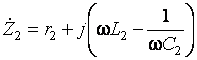 – полное сопротивление второго контура.

Напряжение на катушке индуктивности второго контура:

(5.5)

При резонансе :

(5.6)

Таким образом, очевидны фазовые соотношения напряжений на первом и втором контуре:   опережает  на 90⁰.

При расстройке входной и резонансной частот :

(5.7)

где 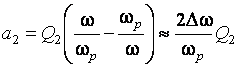 – обобщенная расстройка второго контура.