Он хорошо реализуется на базе нелинейного элемента. Допустим имеется нелинейный элемент на вход которого подаётся управляющее Uy и сигнальное Uc напряжения. Управляющее напряжение много больше сигнального.

Ток, протекающий через нелинейный элемент, можно разложить в ряд Тейлора:
![]()
При малых амплитудах сигнала слагаемыми и степенями «2» и выше можно пренебречь, поэтому:
![]()
Полезная составляющая выходного тока, которая вызывается наличием входного сигнала:
![]()
т.
е. ![]() – диффузионная крутизна ВАХ при заданном управляемом
сигнале.
– диффузионная крутизна ВАХ при заданном управляемом
сигнале.
Такой элемент оказывает сопротивление току: ![]()
Используя такой элемент можно реализовать преобразователь частоты.
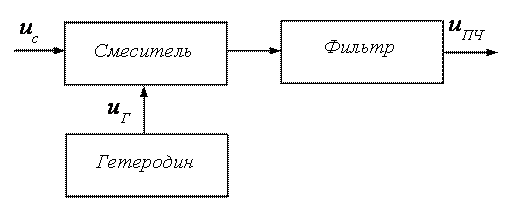

Гетеродин представляет собой генератор гармонического сигнала с постоянной амплитудой. Т. е. управляющее напряжение (Uг) является периодическим, поэтому диффузионная крутизна (Sдиф) изменяется во времени по периодическому закону.
Sдиф может быть представлена рядом Фурье:
![]()
где
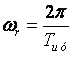
Допустим, что на вход смесителя поступает сигнал с тональной АМ:
![]()
тогда
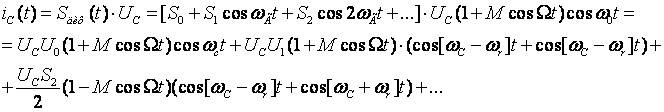
Если в качестве фильтра взять контур настроенный на промежуточную
частоту ![]() и
имеющий
и
имеющий ![]() ,
то на входе контура:
,
то на входе контура:
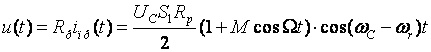
Таким образом, входное напряжение на промежуточной частоте имеет тот же закон модуляции, что и входное напряжение. Такой преобразователь частоты называют линейным. Следует заметить, что описанный преобразователь частоты реагирует одинокого на сигналы с частотами:
![]()
![]()
Преобразователь частоты не фильтрует сигнал зеркального канала и последний оказывает мешающее действие. Для нормальной работы зеркальный канал должен быть подавлен до гетеродина (его частоты).
Для этого перед преобразователем частоты сигнал зеркального канала подавляется во входной цепи приёмника и усилителя высокой частоты.
Для характеристики работы преобразователя используют понятие крутизны преобразования. Оценивая её как отношение амплитуды тока на частоте преобразования к амплитуде немодулированного входного сигнала:
![]()
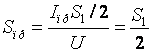
Таким образом крутизна преобразования равна половине амплитуды первой гармоники диффузионной крутизны.
Например, элемент имеет ![]() , а
, а ![]()
Тогда диффузионная крутизна:
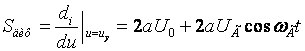
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.