Линейные стационарные цепи. Нелинейные цепи. Параметрические цепи, страница 23

приложенное к нелинейному двухполюснику напряжение

.

Воспользовавшись известными формулами для определения спектрального состава тока необходимо преобразовать первую часть так, чтобы все косинусы были в степени единица. Для этого достаточно воспользоваться следующими соотношениями:

путем подстановки получаем

…

Таким образом, спектр тока кроме составляющей с частотой входного сигнала  содержит постоянную составляющую и гармоники с частотами, кратными частоте входного сигнала. При определении спектрального состава тока удобно пользоваться следующими правилами:

а)  члены полинома с четными степенями формируют в спектре постоянную составляющую и четные гармоники.

б)  члены полинома с нечетными степенями формируют нечетные гармоники.

в)  максимальный номер гармоники соответствует показателю степени членов полинома.

5.2.2  Воздействие гармонического сигнала при кусочно- линейной аппроксимации

ВАХ нелинейного элемента аппроксимируется кусочно-линейно, и работа идёт в режиме большого сигнала.

 

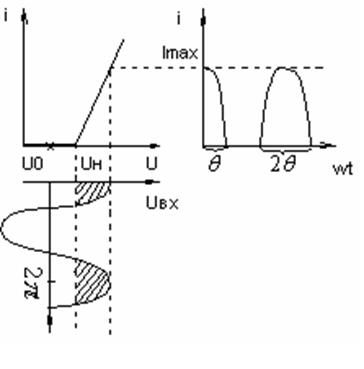Рис. 5.7 Характеристика БНЭ и результат преобразования

U_н – минимальное напряжение, при котором через нелинейный элемент начинает протекать ток.

U₀ – определяет положение рабочей точки на ВАХ.

Ток через нелинейный элемент протекает при условии, когда сумма напряжения смещения и входного сигнала:

.

Ток имеет формулу периодической последовательности импульсов, ширина импульса зависит от угла отсечки θ, который можно найти из условия:

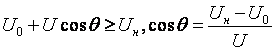
Амплитуда импульсов тока будет равна:

Импульсы тока имеют косинусоидальную форму и могут быть описаны следующим выражением:

Произведем замену: , тогда

Если по оси откладывать x, то ток представляет собой гармоническую последовательность с периодом  и длительностью .

Определим величину I’_m:

, .

Определим спектральную составляющую тока, учитывая, что ток является периодической четной функцией, для нахождения амплитудных составляющих тока достаточно найти коэффициенты ряда Фурье, при функции cos постоянная составляющая:

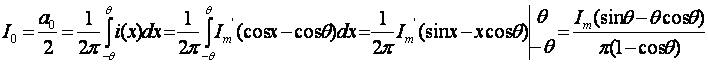
Первая гармоника:

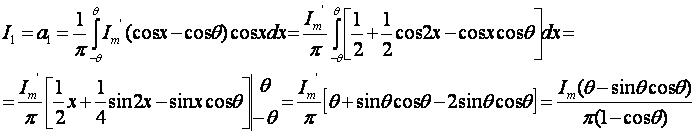
Амплитуда n-гармоники:

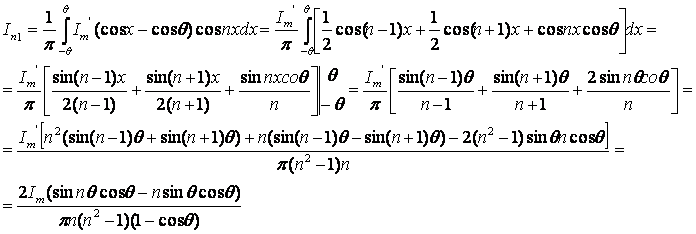
Отношение амплитуды n-ой гармоники к максимальной амплитуде импульса тока называется функцией Берга: