Линейные стационарные цепи. Нелинейные цепи. Параметрические цепи, страница 21

Примером БНЦ может быть биполярный транзистор с проходной характеристикой, приведенной на рисунке 5.1.

 

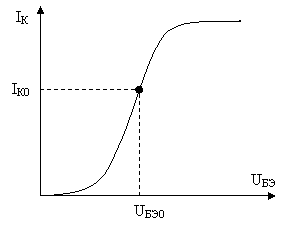Рис. 5.1 Проходная характеристика биполярного транзистора

5.1  Аппроксимация нелинейных характеристик

Оптимальный выбор способа аппроксимации зависит от вида нелинейной характеристики и режима работы нелинейного элемента. На практике для аппроксимации чаще всего используют степенную, кусочно – линейную и показательную функции.

5.1.1  Степенная аппроксимация.

Она основана на разложении нелинейной ВАХ в ряд Тейлора в окрестности рабочей точки, т. е. зависимость i(u) представляется рядом Тейлора:

,

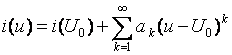где U₀ – рабочая точка (определяется постоянным напряжением)

,

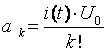т. е. значение соотношений производной в рабочей точке деленной на k!.

 

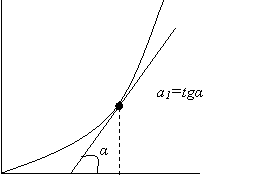
Рис. 5.2 Характеристика БНЭ и ее угол наклона

Коэффициент а₁

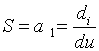 , при u=U₀,

определяет тангенс угла наклона касательной к характеристике в рабочей точке, т. е. это крутизна характеристики в рабочей точке и это есть S . Значение крутизны зависит от положения рабочей точки на характеристике.

Используемые на практике режимы нелинейного элемента:

1.  Режим малого сигнала

Сигнал трансформируется тем или иным участком БНЭ описываемым полиномом 2-го порядка (Рисунок 5.3).

 

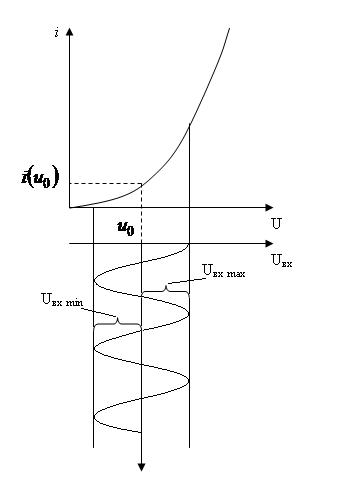
Рис. 5.3 Характеристика БНЭ и ее угол наклона

Например, рабочая точка на начальном участке ВАХ, а входной сигнал мал и не выходит за пределы начального участка. В рассматриваемом случае полином второй степени равен:

i(U₀) – постоянная составляющая, определяющаяся внешним источником (т. е. положением рабочей точки).

Имеется два неизвестных коэффициента a₁ и а₂. Для нахождения a₁ и а₂ необходимо составить систему двух уравнений. Например, можно находить коэффициенты из условия совпадения реальной характеристики и аппроксимирующей функции на границах рабочего диапазона.

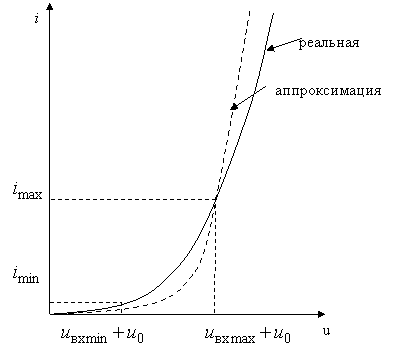
Рис. 5.4 Характеристика БНЭ и ее аппроксимация

На практике часто коэффициент a₁ берут равным крутизне характеристики в рабочей точке S, коэффициент а₂ находят из условия равенства тока нулю при определенном напряжении u_н.