Линейные стационарные цепи. Нелинейные цепи. Параметрические цепи, страница 18

3.5  Влияние обратной связи на нелинейные искажения

Усилительные элементы имеют нелинейные ВАХ, это приводит к нелинейным искажениям, заключаются в том, что в структуре выходного сигнала появляются гармонические составляющие, отсутствующие в спектре входного сигнала. Для уменьшения нелинейных искажений можно применять ООС. Сигнал с искажениями поступает на вход цепи в противофазе и, в силу принципа суперпозиции, усиливается меньше, чем полезный входной сигнал. Повышая глубину ООС нелинейность можно уменьшить очень сильно, но пропорционально нужно повышать коэффициент усиления основной цепи.

3.6  Устойчивость линейных цепей с обратной связью

В реальных цепях с ОС всегда присутствуют паразитные реактивные элементы, создающие дополнительный фазовый сдвиг. Эти фазовые сдвиги могут приводить на некоторых частотах к превращению ООС в ПОС. В результате чего в схеме будут созданы условия для возникновения паразитной генерации, т. е. схема будет неустойчивой. Следовательно, применение ОС связано с проблемой обеспечения устойчивости цепи. Рассмотрим автономную цепь с ОС (Рисунок 3.5).

Входное и выходное напряжения связаны выражением:

(3.20)

(3.21)

 

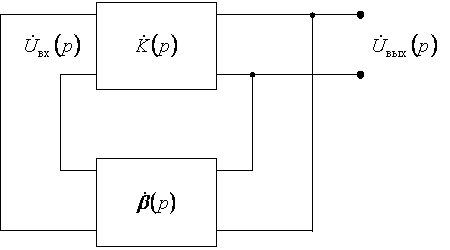Рис. 3.5 Автономная цепь с ОС

Следовательно

(3.21)

Приведённое уравнение называется характеристическим уравнением цепи с ОС. Пусть корни характеристического уравнения равны р₁, р₂… и т. д. В этом случае в линейной системе выходной сигнал можно представить в виде суммы:  

,

1) если корни р вещественные, выходное напряжение будет возрастать или убывать в зависимости от знака корня (Рисунок 3.6)

 

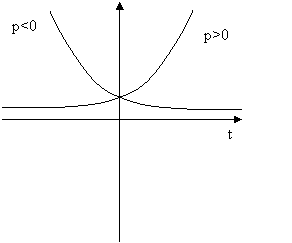Рис. 3.6 Выходное напряжение при действительных корнях

2) если корни р комплексно-сопряженные, выходное напряжение будет иметь колебательный характер, причем огибающая будет возрастать или убывать в зависимости от знака корня (Рисунок 3.7)

Таким образом, корни характеристического уравнения являются вещественными или комплексно-сопряженными, если действительная часть корня является отрицательной (корень лежит в левой полуплоскости), то функция  является убывающей. Если корень лежит в правой полуплоскости, то функция  является возрастающей. Система  будет устойчивой, если при возрастании t , выходной сигнал будет стремиться к 0, для этого корни характеристического уравнения должны лежать в левой полуплоскости,  то есть иметь отрицательные вещественные части.

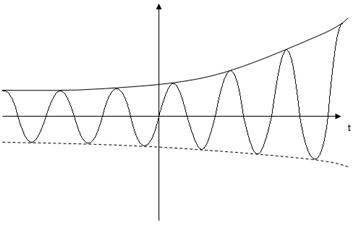
Рис. 3.7 Выходное напряжение при действительных корнях