Линейные стационарные цепи. Нелинейные цепи. Параметрические цепи, страница 36

С помощью параметрической цепи можно осуществить и усиление мощности входного сигнала с понижением его частоты. Можно показать, что это будет иметь место при настройке холостого контура на разностную частоту  и выборе ,  в (6.5). Обычно частота накачки равна удвоенной частоте сигнала, что удобно с практической точки зрения.

7  Синтез линейных цепей

Все задачи можно разделить на задачи анализа и синтеза. При анализе задана структура систем (в виде принципиальной схемы) и необходимо определить характеристики этой системы. При синтезе заданы внешние характеристики системы, а надо определить структуру этой системы. В качестве внешних характеристик выступают: входное сопротивление, частотный коэффициент передачи и т. д.

В настоящее время методы синтеза разрабатываются широко в связи с внедрением средств автоматического проектирования.

Задача синтеза имеет несколько решений, из которых есть хорошие и плохие. Можно задать некоторый критерий и выбрать наилучшее решение. Такой синтез называется оптимальным. Критерии оптимальности могут быть различными, например, минимальное число элементов схемы, минимальная чувствительность к выбору номиналов элементов. Оптимальный синтез носит, как правило, прикладной характер. Общий характер имеет синтез линейных двухполюсников и четырёхполюсников.

7.1  Синтез линейных двухполюсников

Рассмотрим критерии, позволяющие судить о принципиальной возможности или не возможности реализации двухполюсника. Сопротивление двухполюсника может быть записано в виде:

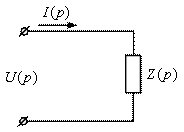
(7.1)

(7.2)

Критерии:

1. Для абсолютно устойчивого пассивного линейного двухполюсника нули и полюсы должны лежать только в левой полуплоскости, т. е. действительная часть   ,  ; , . Если двухполюсник чисто реактивный, то отсутствие потерь энергии ведёт к тому, что нули и полюсы лежат на мнимой оси.

2. Число нулей и полюсов входного пассивного двухполюсника не может отличаться больше, чем на единицу, т. е. . Это означает, что при стремлении частоты к бесконечности пассивный двухполюсник ведет себя либо как индуктивность, при

,

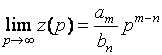Либо как ёмкость , либо резистор .

3. Если в сопротивлении выделить мнимую и вещественную часть , то оказывается, что они связаны между собой преобразованиями Гильберта. Эта связь между вещественной и мнимой частью позволяет оценить поведение сопротивления двухполюсника на всей оси частот. Например, из этого следует, что входное сопротивление двухполюсника и входная ёмкость  удовлетворяют следующему неравенству:

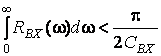
Неравенство позволяет утверждать, что невозможно создать усилитель, имеющий входную ёмкость 10 пФ и входное сопротивление 1Мом в полосе частот от 0 до 1 МГц: