Линейные стационарные цепи. Нелинейные цепи. Параметрические цепи, страница 19

К сожалению, нахождение корней характеристического уравнения для систем высокого порядка является сложной задачей (имеется ввиду требуется много времени для решения задачи). На практике для анализа устойчивости цепи используют критерии устойчивости, которые не требуют решения уравнения.

3.7  Алгебраический критерий устойчивости

Для цепи с сосредоточенными параметрами передаточные функции можно представить в виде отношения полиномов с вещественными коэффициентами:

,

,

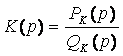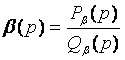Тогда характеристическое уравнение:

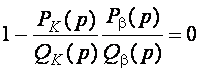
Многочлены с вещественными коэффициентами, все корни которых находятся в левой полуплоскости, называются многочленами Гурвица Н(р). Для определения местонахождения корней многочлена необязательно его решать, для этого достаточно проанализировать коэффициент уравнения.

Так согласно критерию Рауса – Гурвица, для того, чтобы уравнение  с вещественными коэффициентами имело корни, лежащие в левой полуплоскости переменной р, необходимо и достаточно, чтобы положительными  были следующие величины:

а) коэффициенты   … ;

б) определитель Гурвица:

в) все главные миноры определителя Гурвица. Главный минор можно получить вычеркиванием строк и столбцов определителя с одинаковыми номерами (1 строку, 1 столбец или 1 и 3 строку и 1 и 3 столбец).

Алгебраические критерии используют для экономии времени, но они также требуют знания передаточных функций как основного четырехполюсника так и четырехполюсника ОС.

3.8  Частотный критерий устойчивости Найквиста

В характеристическом уравнении произведение является передаточной функцией разомкнутой системы, содержащей последовательно соединенный основной ЧП и ЧП обратной связи (Рисунок 3.8).

 

Рис. 3.8 Выходное напряжение при действительных корнях

Об устойчивости цепи после замыкания связи можно судить по амплитудно-фазовой характеристике разомкнутой системы, которая называется годографом Найквиста.

Критерий устойчивости получил название критерий устойчивости Найквиста. Он формулируется так: если годограф передаточной функции разомкнутой системы не охватывает точку (1, j0), то после замыкания цепи ОС система остаётся устойчивой. В противном случае неустойчивой.

Годограф строится в комплексной плоскости (Рисунок 3.9). Длина вектора соединяющего любую точку годографа с началом координат равна модулю передаточной функции

Угол образуемый вектором и действительной осью равен фазе передаточной функции

 

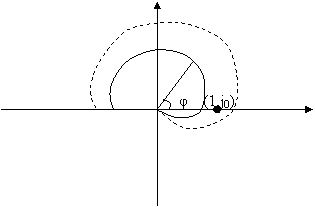Рис. 3.9 Годограф Найквиста

 При сложной форме годографа часто бывает трудно судить об охвате им точки (1, j0), в этом случае удобно использовать следующее правило: система с обратной связью устойчива, если годограф не пересекает действительную ось правее единицы; либо пересекает эту ось одинаковое число раз в положительных и отрицательных направлениях.