Линейные стационарные цепи. Нелинейные цепи. Параметрические цепи, страница 33

Отсюда:

Таким образом, крутизна преобразования пропорциональна амплитуде напряжения гетеродина.

6.2  Параметрические ёмкостные элементы

Параметрическая ёмкость достаточно просто реализуется на специальном полупроводниковом диоде, который называется варикап. Параметрическая ёмкость, используемая в высокочастотном диапазоне, иногда называется варактором. Если к полупроводниковому диоду приложить напряжение обратной полярности, то величина заряда в области запирающего слоя зависит от приложенного напряжения. Полученная зависимость называется вольт-кулонной характеристикой параметрического конденсатора (ВКХ). Если изменять приложенное напряжение, то ток через диод (ток смещения) будет равен:

С_диф(u) – диффузионная ёмкость конденсатора, она зависит от приложенного напряжения следующим образом:

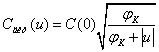
С (0) – ёмкость

φ_к – контактная разность потенциалов, которая зависит от кристалла, примеси и других факторов.

Современные варикапы работают на частотах до 10 ГГц, в миллиметровом диапазоне волн.

Рассмотрим зависимость между ёмкостью конденсатора и запасённой в нём энергии. Пусть имеется плоский конденсатор, расстояние между пластинами равно – х, площадь пластин S, и конденсатор заряжен до напряжения u. Тогда ёмкость конденсатора будет равняться:

Заряд:

Энергия, запасённая в конденсаторе будет равняться:

Рассмотрим изменение энергии при q = const:

Таким образом, если заряд остаётся постоянным, то запас энергии в конденсаторе возрастает при уменьшении ёмкости, и уменьшается при её увеличении, т. е. изменение энергии, запасённой в конденсаторе, происходит за счет работы, совершаемой при перемещении обкладок.

Для увеличения энергии, запасённой в конденсаторе, необходимо за счет внешних сил уменьшить ёмкость заряженного конденсатора. Если ёмкость изменять периодически, то средняя энергия, запасённая в конденсаторе, изменяться не будет, т. к. на интервалах уменьшения ёмкости энергия в конденсаторе возрастает, а на интервалах увеличения ёмкости уменьшается на ту же величину.

Однако энергию, запасённую в конденсаторе, можно изменять, если напряжение на конденсаторе изменяет знак, т. е. проходит через ноль.

Рассмотрим высокодобротный колебательный контур, в котором ёмкость изменяется во времени С(t). Будем считать, что напряжение на ёмкости изменяется по гармоническому закону, это возможно, если в контуре возбуждены собственные колебания, частота которых вычисляется по следующей формуле:

где С₀ – ёмкость при нулевом приложенном напряжении.

Предположим, что ёмкость изменяется скачком, причём в моменты прохождения напряжения на ёмкости через нулевое значение ёмкости увеличивается, а в моменты, когда напряжение достигает максимального значения, величина ёмкости уменьшается:

В моменты, когда = 0 (момент увеличения ёмкости), энергия запасённая в конденсаторе равна нулю, т. к.  , поэтому при увеличении ёмкости её энергия не изменяется (следовательно ).