Линейные стационарные цепи. Нелинейные цепи. Параметрические цепи, страница 20

Для определения устойчивости годограф строить необязательно. Для этого достаточно проанализировать АЧХ и ФЧХ. Следовательно, третья альтернативная формулировка критерия Найквиста: если АЧХ больше единице на частотах, при которых ФЧХ равна 0 или  где n €  z, то система с обратной связью не устойчива, в противном случае устойчива (Рисунок 3.10).

 

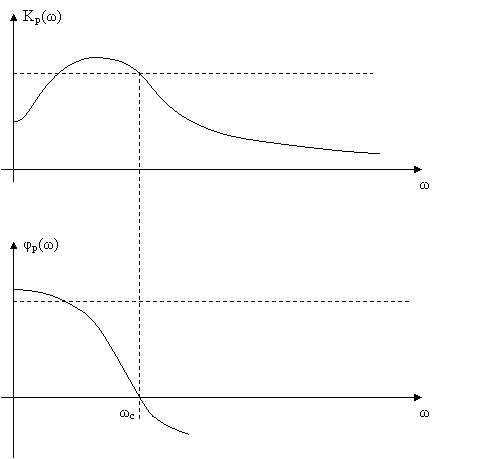Рис. 3.9 АЧХ и ФЧХ разомкнутой системы с обратной связью

4  Прохождение случайных сигналов через линейные стационарные цепи

Основными характеристиками случайного процесса является плотность вероятности мгновенных значений сигнала, корреляционная функция и спектральная плотность мощности. Отыскание плотности вероятности мгновенных значений сигнала на выходе линейной цепи по известной плотности вероятности на входе цепи и известным характеристикам цепи представляет весьма сложную задачу. Однако, если входной сигнал является гауссовым, то выходной сигнал так же всегда будет гауссовым. Это означает, что решение задачи упрощается и сводится к нахождению параметров выходного сигнала (математического ожидания и дисперсии).

Задача нахождения корреляционной функции и спектральной плотности мощности выходного сигнала значительно проще.

Обратные преобразования Фурье от спектральной плотности мощности согласно теории Винера – Хинчина:

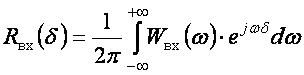 – корреляционная функция сигнала

Обратные преобразования Фурье от коэффициента передачи по мощности:

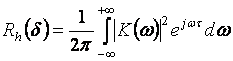 – корреляционная функция импульсной характеристики сигнала

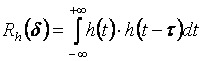
Так как произведение спектров двух сигналов равно спектру свёртки этих сигналов, то можно записать:

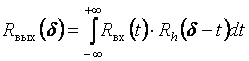
То есть корреляционная функция сигнала на выходе линейной цепи равна свёртке корреляционной функции сигнала на входе цепи и корреляционной функции импульсной характеристики цепи.

При анализе различных систем в качестве помехи часто выступает белый шум, имеющий спектральную плотность мощности постоянную во всём диапазоне частот:

 и корреляционная функция

Тогда

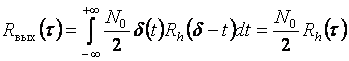
Следовательно, корреляционная функция выходного сигнала равна автокорреляционной функции импульсной характеристики с коэффициентом .

5  Прохождение сигналов через нелинейные цепи

Линейные стационарные цепи не изменяют спектральный состав сигнала. Основные радиотехнические преобразования, связанные с изменением спектрального состава сигнала, осуществляется либо с помощью нелинейных цепей, либо линейных цепей с переменными параметрами.

Исследование нелинейных цепей представляет собой сложную задачу, состоящую в решении нелинейных дифференциальных уравнений. Анализ нелинейных цепей упрощается, если нелинейный элемент является безынерционным, т. е. реакция на изменение входного воздействия происходит мгновенно. Строго говоря, безынерционных элементов (БНЭ) нет, но в случае, когда время изменения входного сигнала значительно превышает время установления процесса в нелинейном элементе, элемент может считаться безынерционным. В радиотехнике в качестве нелинейных элементов чаще всего используют полупроводниковые приборы (диоды, транзисторы). Для описания таких приборов используют ВАХ, которые связывают между собой напряжения, приложенные к приборам и токи, протекающие через приборы.