Основи теорії захисту інформації: Конспекти лекцій № 1-32 (Введення в криптологію, основні поняття і визначення. Проблеми теорії і практики криптології), страница 9

DES – алгоритм, у ньому :

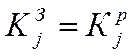                                                                                           (1)

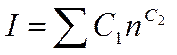                                                                                    (2)

RSA – (Рівер, Шаміль, Отаман) – складно обчислити ключі один з іншого.

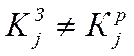                                                                                           (3)

Сутність алгоритму - він є блоковим, у ньому повідомлення М розбивається на блоки Мi, з довжиною блоку  (768 біт мінімум), реально 1024, 2048.

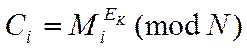                                                                        (4)

 - ключ прямого перетворення .

                                                                                            (5)

P, Q – великі прості числа.

                                                              

Дешифрування за правилом:

                                                                           (6)

Дк - ключ зворотного перетворення .

Підставимо (4) у (6):

                                                  

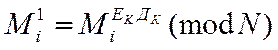
Використовуючи теорію порівняння:

                                                                        (7)

Якщо (7) має єдине рішення, тобто існує єдина пара , то такий шифр є однозначним.

Генерація ключів (задачі)

1.  Генерація випадкової пари .

2.  Генерація P і Q, що задовольняє умові (5).

3.  RSA відноситься до системи з відкритими ключами, що порозумівається тим, що ключі  поділяються на двох частин.

c     - з'являється конфіденційним (особистим).

                   - відкритий (публічний) для шифрування навпаки.

Усі параметри (N,P,Q) також поділяються на 2 класи: N – відкритий, P,Q - конфіденційний (секретний).

Сутність моделі взаємної недовіри – кожен користувач генерує ключі сам собі. Особистий ключ залишає в себе і забезпечує його строгу конфіденційність. Відкритий ключ розсилає всім користувачам, з якими він зв'язаний. Він також забезпечує цілісність і дійсність відкритих ключів.

 - повинні вибиратися з повної множини випадково, порівняно ймовірно і незалежно, повинні забезпечувати однозначну оборотність прямого зворотного перетворення.

                                                       

                                                                                                        (8)

(7) можна звести до Діфантового рівняння:

                                                                   ax+by=1                                (9)

Діафантове рівняння – нормоване, тому що праворуч коефіцієнт = 1, a, b – цілочисельні коефіцієнти, х, у – невідомі.

                                                                      (10)

k – деяке невідоме число

 можна згенерувати випадково.

Діафант. рівняння має цілочисельне рішення, якщо a  і  b цілочисленні, і a ≥ b, a  і  b взаємно прості.

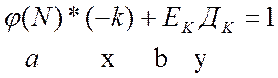                                                                 (11)

Одним з найбільш швидких рішень (11) є ланцюгові дроби.

                                                        

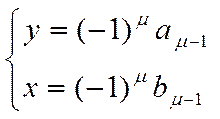
де  ? – порядок ланцюгового дробу,  a  і  b – параметри ланцюгового дробу.

Знаходимо параметри:

a/b  представляється у виді ланцюгового дробу.

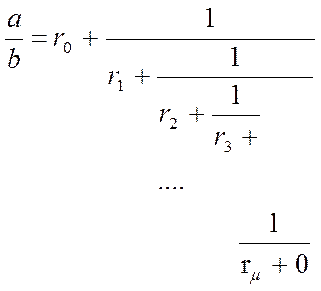                                                          (12)

μ  - порядок ланцюгового дробу, перший коефіцієнт, у якого залишок дорівнює 0.

                                                                      

                                              

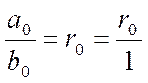
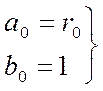
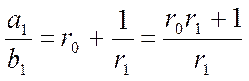
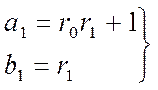
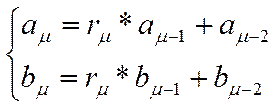                                                                 (13)

При великих N – велике значення μ.    μ ≈ ⅓ N.

Оцінка стійкості і складності

RSA – доказово стійка система (криптоалгоритм). Основною задачею для RSA є перебування ( ) і параметрів.

Кількість пар  для заданого N :

                                              (14)

Очевидно, якщо P-1 і Q-1 d великі й у канонічному розкладанні мають мало співмножників, то кількість ключів буде максимізоване.

Числа P і Q повинні бути не просто простими, а сильними простими числами (у вузькому змісті), тобто мати вид: