- еквівалент у групах точок ЕК заміняється скалярним множенням.
![]() (8)
(8)
у (8) d – число, G – базова точка на ЕК![]() породжує групу точок n – порядку.
породжує групу точок n – порядку.
чи
![]() (9)
(9)
у (9) d – особистий секретний ключ = х.
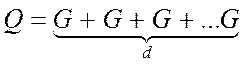 (10)
(10)
При виконанні (10) виділяють 2 операції: операція подвоєння – складається 2 однакові точки, і операція додавання – складаються 2 різні точки.
![]()
![]() (11)
(11)
на ЕК сума цих точок:
![]() (12)
(12)
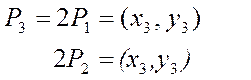 (13)
(13)
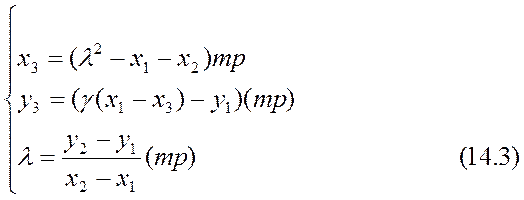 (14)
(14)
(14) – визначає метрику додавання 2 точок.
точно також для подвоєння, але (14.3) заміняємо (15):
 |
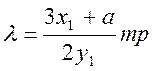 (15)
(15)
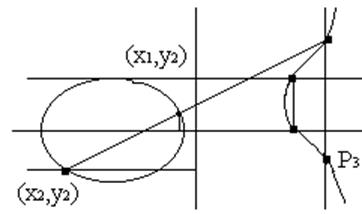
Рис.14.1
на ЕК є точка ОБ – нейтральний елемент, точка нескінченності.
Приклади:
Нехай мається ЕК.
![]()
а = 1, б = 1, Р = 23
1. Перевірити, що наступні точки: (1,7), (1,16), (3,10), (3,13), (4,0), (5,4), (5,19), (6,4), (6,19), (7,11), (7,12), (9,7), (9,16), (17,3), (17,20), (18,20), (19,5), (13,16) належать ЕК.
P1=(3, 10) P2=(9, 7)
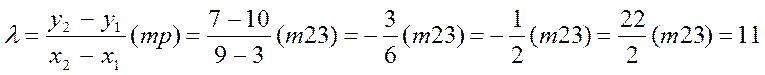 |
![]()
![]()
Р3=(17,20)
(частина 2)
1. Афінні і проективні базиси.
2. Приклади перетворень.
3. Порівняння перетворень у полях, кільцях, еліптичних групах.
Відомо 2 представлення груп точок ЕК, 2 базиси: афінний і проективний.
Для поля ![]() ,
, ![]()
![]() (1)
(1)
де ![]() - точки ЕК
- точки ЕК ![]()
а, б – параметри ЕК, ![]()
У порівнянні (1) ![]() , а також а, b – коефіцієнти, є поліномами не вище m – порядку.
, а також а, b – коефіцієнти, є поліномами не вище m – порядку.
m
![]() 2
2 ![]()
![]()
m³160 ![]() .
.
Афінний базис вимагає великої обчислювальної складності.
![]() (2)
(2)
![]() - базова точка.
- базова точка.
d – особистий секрет ключа ![]()
n – порядок (період) базової точки G.
![]()
Для зменшення чи складності підвищення швидкості використовується проективний базис:
X,Y,Z
при цьому перехід з афінного представлення в проективний:
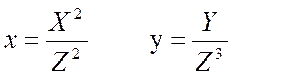 (3)
(3)
підставимо (3) у (1).
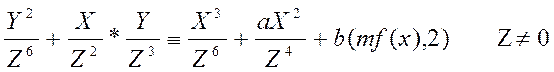
![]() (4)
(4)
(4) задає ЕК над полем ![]() у проективному базисі.
у проективному базисі.
(X,Y,Z) – кожна точка задається трьохмірно.
Метрика 2 над полем ![]()
Нехай відомі координати 2 точок:
![]()
![]()
![]()
![]()
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
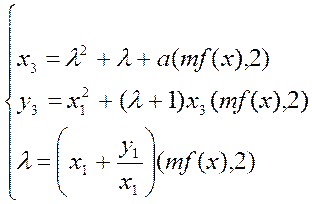 (8)
(8)
У (7), (8) усі параметри – поліноми не вище m– того ступеня.
F(x)- примітивний поліном над ![]() .
.
Примітивність ![]() - max період поля буде
- max період поля буде ![]() елементів.
елементів.
Загальносистемні параметри перетворень на ЕК
1. Методи побудови простих чисел і примітивних поліномів.
2. Побудови і властивості базових точок на ЕК.
3. Характеристика методів, визначення порядку в ЕК.
1) q – порядок поля
![]()
2)
![]()
3)
![]() ,
n – просте число, порядок точки G.
,
n – просте число, порядок точки G.
n(modq)º0
4) U повинно бути майже простим,
![]()
Р ![]()
Усі методи побудови простих чисел можна розділити на 3 класи:
1) аналітичні
2) "псевдопрості"
3) гіпотетичні (на основі гіпотез)
До аналітичного відносяться методи, на основі яких можна побудувати строго простt число.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.