Основи теорії захисту інформації: Конспекти лекцій № 1-32 (Введення в криптологію, основні поняття і визначення. Проблеми теорії і практики криптології), страница 27

Методи розподілу:

Метод спробного розподілу

Якщо 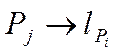, то тоді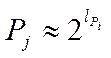

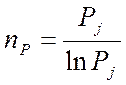                                                                                             (3)

1.  метод r - Поларда

2.  метод r-1 Поларда

3.  метод факторизації на ЭК

4.  двійкове решето

5.  загальне решето числового поля

Двійкове решето

429 біт – 129 дес. числ.

Ефективний, якщо

Сутність:

Є цілі Х и У, такі, що:

                                                                     (4)

                                                        

                                                                                           (5)

k=1,2….

                                                                               (6)

                                                                     N=P*Q

Вираз (6) означає , що:

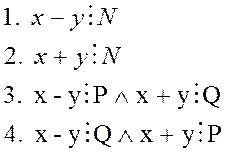                                                                             (7)

1 і 2 не дозволяють знайти P і Q.

3 і 4 дає рішення.

х-у∶Р, те ми можемо скористатися алгоритмом Евкліда перебування НСД.

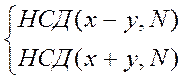                                                                                    (8)

(8) дозволить знайти P чи Q.

1.  Нехай N – число, яких необхідно факторизувати. Побудуємо деяку базу , з таким значенням, щоб .

 - прості числа невеликого розміру.

Z – база двоійкового решета.

2.  Знайдемо , округлимо його знизу. Потім побудуємо числа виду  і знайдемо . У результаті одержимо рівняння:

                                                    

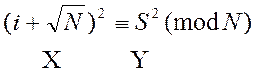
Приклад.

N=209    Z=P

Побудуємо базу

Знайдемо

Результати зведемо в таблицю:

i			2	3	5	7
1 2 3 .. .. 16	1+14=15 16 17 30	47	4 - 4 6	- - - -	- - 1 -	- - - -	+ - + +

 x      y

х = 15                            

у = 4

Р = 19

Q=N/P=209/19=11

На практиці при великих N матриця таблиці має велику величину. Для

, потім комбінуючи рядка, у яких + (розкладання по базисі виконане) необхідно домогтися .

Метод r - Поларда

У методі r - Поларда також шукаються 2 числа Х и У, що . У цьому випадку:

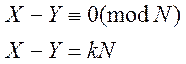
Якщо числа Х и У обрані правильно, то можна шукати НСД(X-Y,N). У цьому методі рекомендують Х и У формувати випадково.

Приклад.

N=209

f(x)=x²+1(mod N)

xo=17

   

Лекція №22

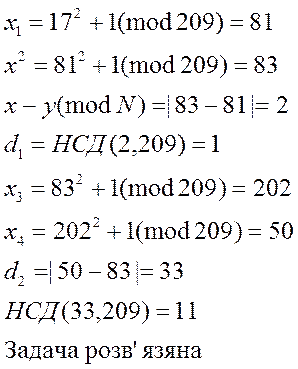
Стійкість криптосистем класу Діфі - Хелмана, Ель - Гамаля і ЕК.

1.  Загальна характеристика методів Поларда.

2.  Рішення дискретного логарифмічного рівняння.

3.  Особливості рішення дискретного логарифмічного рівняння.

1.  Загальна характеристика методів Поларда.

Стійкість криптосистем Діфі - Хелмана й Ель - Гамаля базуються на складності рішення дискретного логарифмічного рівняння виду:

                                                                                                      (1)

                                                                                   (2)

Для рішення здійснюється припущення, що Y_i, P, а – відкриті параметри.

Дискретний логарифм на ЕК:

 ,                                                                         (3)

де Р- простe число.

З (3) варто визначити d – секретний ключ відправника.

Вважається, що КРА відомо загальносистемні параметри. Розглянута атака полегшена тому що атаку здійснює внутрішній користувач.

Методи Діфі - Хелмана, Ель - Гамаля і ЕК, є доказово стійкими, а доказом стійкості є складність рішення порівнянь (1) - (2).

Сутність методу - Поларда полягає в тому, що використовується деяка функція  за допомогою якої формується безліч крапок :

                                                                                                  (4)

Аналогічно для ЕК будується безліч крапок :

                                                                                         (5)

Звичайно при рішенні таких порівнянь, крива - Поларда має вид: