Основи теорії захисту інформації: Конспекти лекцій № 1-32 (Введення в криптологію, основні поняття і визначення. Проблеми теорії і практики криптології), страница 28

Особливістю цієї кривої є те, що точки зациклення , є рішенням задачі дискретного логарифма. Тобто якщо ми будуємо криву й одержуємо в деякій крапці збіг координат, чи індексів ступенів. Тому що параметри дуже великі, то ймовірність того, що ми дійдемо до зациклення, дуже мала.

Для ухвалення рішення потрібно порівняти кожне поточне значення Р_j з попередніми значеннями. Всі отримані значення необхідно десь зберігати. Такого класу задачі, як порівняння крапок з попередніми, називають задачею Флойда.

 Сутність рішення полягає в тім, що фіксується деяке значення - точка і всі точки далі ми порівнюємо з цією крапкою.

                                                                         (6)

У цьому виразі розуміється те, що збіглися, наприклад, індекси ступені.

Можливим є вибір чи кроку відстані між точками.

2.  Рішення дискретного логарифмічного рівняння.

Чисто з інтуітивних розумінь функцію  запропонували формувати у виді лінійної комбінації базової точки G і відкритого ключа Q:

 ,                                                                                                        (7)

де - коефіцієнти що дозволяють формувати  точку.

Тому що ми шукаємо рішення d, те , де n- порядок базової точки на ЕК.

Першу базову точку задаємо як:

                                                                                                     (8)

Припустимо ми реалізуємо метод Флойда, обчислюємо -точку:

                                                                                                (9)

Припустимо, що на j-тім кроці нам повезло, тобто:

                                                                                                           (10)

Це дозволяє нам дорівняти (7) і (9):

                                                                                    (11)

Звідси знайдемо Q:

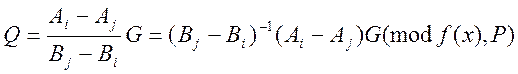                                        (12)

Порівняємо (3) і (12), з порівняння випливає, що:

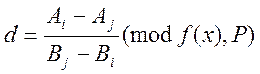                                                                                             (13)

Висновок: очевидно, що для рішення порівняння (13) потрібно знайти безліч коефіцієнтів , при яких виконується умова (11).

Побудуємо точки  використовуючи метод -метод, при цьому використовуючи правило:

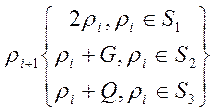                                                                              (14)

При цьому зафіксуємо деяке початкове положення  .

Область S визначається над безліччю значень . Для реальних значень число областей розбивок, повинне бути не менше ніж 20.

Приклад:

Нехай базова точка G=(13,7). Ця точка належить ЕК:

 

для такої ЕК можна показати, що порядок базової точки n=7, u=4*7=28 – порядок ЕК.

Нехай також відомо, що Q=(17,20). Необхідно вирішити ключове порівняння:

 .

Розіб'ємо область S на три підгалузі: . Далі будемо формувати функцію (14) використовуючи це правило:

 . Розподіл будемо здійснювати по - ий координаті.

 

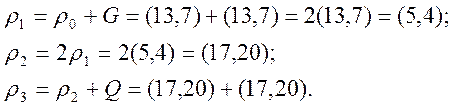
Точка .

Далі необхідно знайти коефіцієнти  при який відбувся збіг:

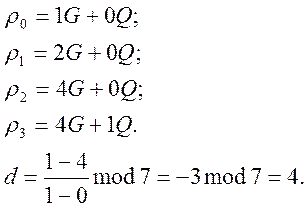
3.  Особливості рішення дискретного логарифмічного рівняння.

Нехай необхідно вирішити дискретне логарифмічне рівняння:

                                                                                                        (15)

Скористаємося методом Поларда, і будемо вважати, що ми знайшли деяку пару параметрів (u,v) і (t,w), що:

                                                                                            (16)

 

Підставимо в порівняння (16) значення b з (15):

                                                                                                        (17)

                                                                                       (18)

У рівняння (18) можна прирівняти показники, але по модулі функції Ейлер від , тобто:

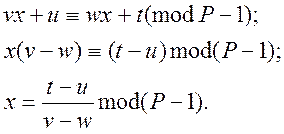
Ми одержали те ж, що і (13).

За допомогою - методу Поларда сформуємо значення , тобто задамо правило аналогічне з правилом розподілу на область:

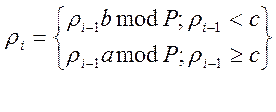,                                                                                      (19)

 де .

Для рішення дискретного логарифма виду (15) метод - Поларда дуже обчислювально складний. Існують більш швидкі методи, наприклад загальне решето числового полючи.