2. Методи оцінки стійкості ймовірно стійких криптосистем.
Основним методом оцінки стійкості системи є перевірка складності рішення деяких задач.
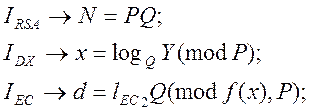
Складність задач RSA оцінювана в групових операціях, можна оцінити як:
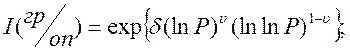 (14)
(14)
З (14) випливає, що складність залежить від величини ![]() і від
і від ![]() -
характеристики методу факторизації. Якщо факторизація здійснюється методом
двоійкового решета, то
-
характеристики методу факторизації. Якщо факторизація здійснюється методом
двоійкового решета, то ![]()
Якщо для рішення дискретного логарифма
використовується загальне решето числового полючи, то складність рішення
дискретного логарифма носить також суб експоненціальний характер, але ![]() .
.
Для ЕК складність рішення задачі дискретного еліптичного рівняння, визначається операцією додавання в ЕК:
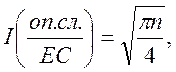 (15)
(15)
де ![]() -порядок точки на ЕК.
-порядок точки на ЕК.
Лекція № 24
Методи криптоаналізу симетричних блокових криптоалгоритмів
1. Особливості рішення порівняння для дискретного алгоритму.
2. Характеристики методів криптоаналізу блокових симетричних шифрів (БСШ).
3. Сутність криптоаналізу БСШ.
4. Сутність диференціального криптоаналізу.
Приклад:
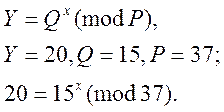
Необхідно знайти х.
Використовуємо метод Поліга - Хелмана:
1. Підставляємо число Р-1 у виді канонічного розкладання:
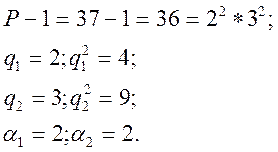
2. Записуємо формулу по який будемо проводити обчислення:
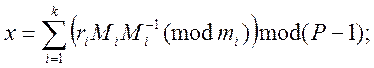
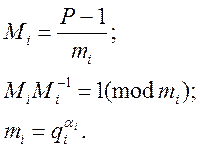
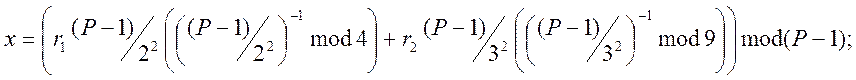
![]() (1)
(1)
![]() (2)
(2)
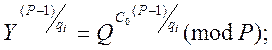
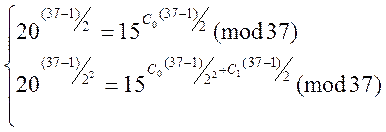 ;
(3)
;
(3)
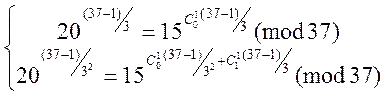 ;
(4)
;
(4)
Підставивши в перше рівняння системи (3)
послідовне значення ![]() , і перевіряємо на порівняння
ліву і праву частини.
, і перевіряємо на порівняння
ліву і праву частини.
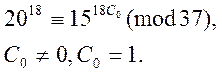
Підставляємо ![]() в друге
рівняння системи (3) одержимо:
в друге
рівняння системи (3) одержимо:
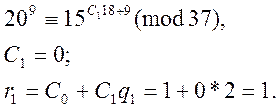
Аналогічно знайдемо ![]() :
:
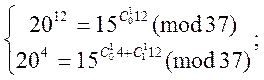
Послідовно підставляючи В рівняння коефіцієнти ![]() ми визначимо, що
ми визначимо, що
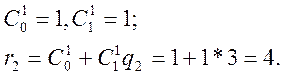
Підставивши значення ![]() й
й ![]() у формулу (1) одержимо:
у формулу (1) одержимо:
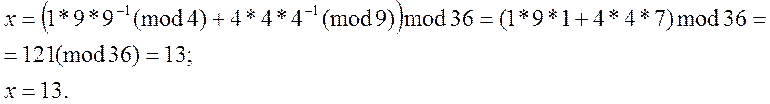
Якщо ![]() , то в цьому випадки
, то в цьому випадки![]() і
і ![]() , що
значать коефіцієнтами є
, що
значать коефіцієнтами є ![]() і
і ![]() . Нам необхідно знайти
. Нам необхідно знайти 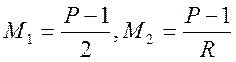 . Далі потрібно вирішити задачу перебування
зворотного елемента
. Далі потрібно вирішити задачу перебування
зворотного елемента ![]() :
:
![]()
Відносно БСШ завжди існує можливість виконання атаки типу «груба сила».
Основними показниками складності цієї атаки є: ![]() .
.
Стосовно до БСШ:
![]() ,
(5)
,
(5)
де ![]() - кількість дозволених у
системі ключів.
- кількість дозволених у
системі ключів.
Більш істотним визначенням складності цієї атаки є ![]() :
:
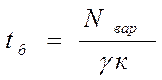 .
(6)
.
(6)
Атаку «груба сила» можна використовувати для оцінки складності інших атак. Наприклад аналітичних атак. Аналітичної будемо розуміти таку атаку, у якій враховують алгоритми шифрування, параметри шифрування і залежності криптограм, ключів і повідомлень між собою.
Для аналітичної атаки складність можна оцінити
кількістю ![]() , деяких групових операцій для здійснення
атаки. Аналогічно можна визначити
, деяких групових операцій для здійснення
атаки. Аналогічно можна визначити ![]() :
:
![]() , за умови
продуктивності системи.
, за умови
продуктивності системи.
2.Характеристики методів криптоаналіза блокових симетричних шифрів (БСШ).
При розробці БСШ ставитися вимога, щоб ніякої аналітичної атаки по відношенню шифру. Цю вимогу формулюють у виді вимоги надійності математичної бази і математичного апарата цього алгоритму.
3.Сутність криптоаналізу БСШ.
Потрібно, щоб алгоритм мав статистичну безпеку. Сутність полягає в тім, щоб криптограми не залежали від повідомлень, і від ключів.
В даний час розроблено велику безліч методів криптоаналізу. Основними є:
1. Диференціальний криптоаналіз.
2. Метод розширення для диференціального криптоаналізу.
3. Пошук найкращої диференціальної характеристики.
4. Лінійний криптоаналіз.
5. Алгебраїчне вторгнення.
6. Вторгнення з частковим угадуванням ключа.
7. Вторгнення зі зв'язаними ключами.
8. Вторгнення на основі обробки збоїв (навмисних) у роботі алгоритму.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.