![]() ,
(15)
,
(15)
де ![]() - початковий j- тий ключ. Тоді
- початковий j- тий ключ. Тоді
![]() . (13)
. (13)
Покладемо, що КРА може перехватити тільки ![]() та
зможе сформувати послідовність
та
зможе сформувати послідовність ![]() (яку-небудь). Тоді він
формує
(яку-небудь). Тоді він
формує ![]() . Будемо вважати, що ЗЗУ має синхронізацію
по і. Тоді відновленням повідомлення отримаємо:
. Будемо вважати, що ЗЗУ має синхронізацію
по і. Тоді відновленням повідомлення отримаємо: ![]() . Таким
чином, нав'язати хибне повідомлення неможливо. Теорему доведено.
. Таким
чином, нав'язати хибне повідомлення неможливо. Теорему доведено.
У більшості відкритих додатків джерело ![]() не
довіряє
не
довіряє ![]() . Більш того, обоє прагнуть захисту від
арбітражу. Це може бути досягнуто, якщо в системі використовується несиметрична
криптографія.
. Більш того, обоє прагнуть захисту від
арбітражу. Це може бути досягнуто, якщо в системі використовується несиметрична
криптографія.
Лекція 14
Методи забезпечення цілісності та достовірності
у класі симетричних шифрів.
Навчальні питання:
1. Методи автентифікації в симетричних потокових системах.
2. Методи автентифікації в блокових симетричних системах.
1. Методи автентифікації в симетричних потокових системах.
Теорема 14.1.
Використання потокового шифрування та групових кодів, що знаходять та виправляють помилки, є необхідною, але не достатньою умовою забезпечення цілісності та достовірності захищаємої інформації.
Доведення. Нехай М – інформація. ![]() –
блоки інформації М. При груповому кодуванні обчислюються контрольні символи як
–
блоки інформації М. При груповому кодуванні обчислюються контрольні символи як
![]() (1)
(1)
Після цього в систематичному груповому коді шкірному блокові додається
КС: ![]() . На прийомній стороні в декодері на основі
КС знаходяться та виправляються помилки, якщо їх не більше, ніж виправна
здібність коду. Для захисту
. На прийомній стороні в декодері на основі
КС знаходяться та виправляються помилки, якщо їх не більше, ніж виправна
здібність коду. Для захисту ![]() використовується
поточне шифрування:
використовується
поточне шифрування:
![]() (2)
(2)
Групові коди володіють властивістю, що операція ![]() є
дозволеною комбінацією цього ж коду, тобто властивість замкнутості:
є
дозволеною комбінацією цього ж коду, тобто властивість замкнутості:
![]() .
.
Якщо КРА може нав'язати хибну інформацію методом модифікації, додавши ![]() , то декодер прийме
, то декодер прийме ![]() і
цієї модифікації не виявить її.
і
цієї модифікації не виявить її.
Теорему доведено.
Висновок: у відповідності з Т.14.1 у поточних системах, які використовують групові коди, може нав'язуватися інформація як випадкового так і визначеного змісту.
Теорема 14.2
Необхідною і достатньою умовою забезпечення цілісності та достовірності в системах потокового шифрування є:
- використання потокового шифрування;
- використання групових кодів, виявлення помилок;
-
формування ![]() шифруючої з використанням раніше
переданих символів криптограми або відкритої інформації.
шифруючої з використанням раніше
переданих символів криптограми або відкритої інформації.
Рис.14.1. – 14.2
Роздивимося на рис. 14.1, 14.2
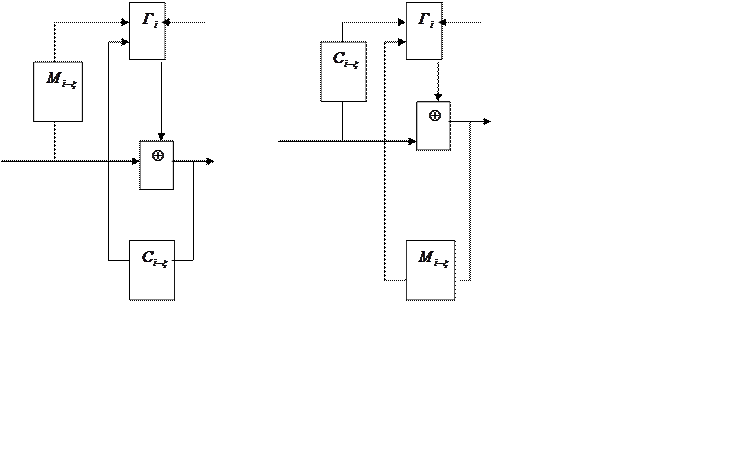 |
де ![]() (5)
(5)
у нашому випадку зашифрування ![]() (6)
(6)
розшифрування 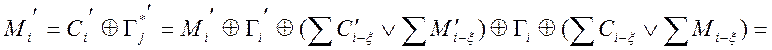
![]()
![]() -
- ![]() , яку
сформоване на приймачі.
, яку
сформоване на приймачі.
Якщо ![]() , тобто сформувати правильно, то
, тобто сформувати правильно, то ![]() . І вирази з сумами відповідно =0
. І вирази з сумами відповідно =0 ![]()
![]() - це значити
інформацію прийняли правильно.
- це значити
інформацію прийняли правильно.
Якщо ![]() , то
, то ![]() - не
правильно.
- не
правильно.
Наприклад, розшифрувати з помилкою ![]() затримується
і приймають доля у формуванні
затримується
і приймають доля у формуванні ![]() . Це приводити до
неправильного розшифруванню.
. Це приводити до
неправильного розшифруванню.
![]() Кодові комбінації автоматично виявив факт
появи помилки і автоматично відмовляється від цієї інформації
Кодові комбінації автоматично виявив факт
появи помилки і автоматично відмовляється від цієї інформації ![]() нав'язування не відбувається.
нав'язування не відбувається.
2. Методи автентифікації в блокових симетричних шифрах.
Здійснюється на основі обчислення для шкірного блоку криптографічної контрольної суми. КАС
![]() (7)
(7)
Імітовставка формується як з використанням Кш, так і з використанням Kа. Алгоритм обчислення КАС, показане на рис. 14.3.
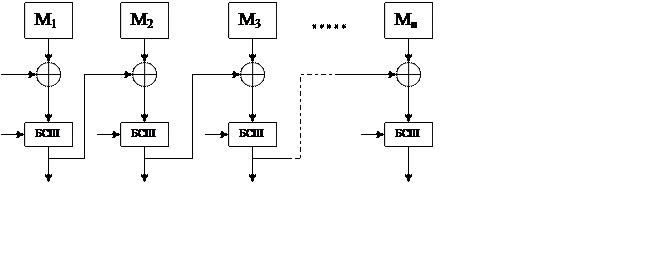 |
Імітовставка залежить від усіх блоків даних, смороду беруть доля в її формуванні (це видно з малюнку 14.3).
Таким чином цілісність та достовірність можуть бути забезпечені тільки за рахунок введення збитковості. Для потокового шифрування – у вигляді контрольних кодових комбінацій, а для блокових – у вигляді імітовставки.
Перевірка цілісності:
Прийняте повідомлення разом з імітовставкою перетворюється так:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.