Основи теорії захисту інформації: Конспекти лекцій № 1-32 (Введення в криптологію, основні поняття і визначення. Проблеми теорії і практики криптології), страница 7

                                            (11)

                                                                                (12)

                                                                         (13)

Якщо S=0 у шифрі, то такий шифр називається лінійним афінним шифром, якщо в шифрі а=1, то шифр називається шифром зрушення. Більшість шифрів вкладається в клас афінних шифрів.

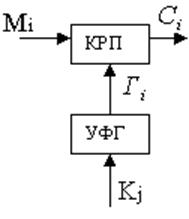
У потокових криптоперетвореннях об'єктами взаємодії є символи повідомлення Мi і символи ключа Kj, причому з використанням символів ключа формується Гi.

                                                   Мi ,       Kj ,         

                                                                      (14)

Рис 5.1

* - множення, + , - ;

Розшифрування:

                                                                     (15)

При обчисленні необхідно строго синхронізувати по i, тобто: Гi  при розшифруванні і зашифруванні та сама.

М – ічне шифрування (по mod).

Приклад:

                                                                                                                                                    

Двійкове гамування

                                                                             

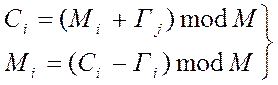
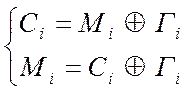
Гi повинна породжуватися псевдовипадковим чи випадковим процесом. Реалізація процесу повинна залежати від вихідного ключа.

Правильне розшифрування в (18), (19) за умови, що відправник і одержувач використовують той самий ключ, вони можуть сформувати однакові гами. Необхідно забезпечити синхронізацію по i.

Блоковими перетвореннями називаються такі шифри, при яких інформація М поділяється на блоки Мi по в кожнім із блоків. Кожний із блоків зашифровується з використанням того самого ключа.

Блокове шифрування можна реалізувати за рахунок:

1)  використання операцій перестановки символів у блоці за законом ключа;

2)  підстановки (чи заміни) замість символів повідомлення інших символів, що задаються ключем;

3)  за рахунок використання в загальному випадку афінного перетворення (11), (12), якщо Мi – символи розглядати як блоки;

4)  за рахунок використання операції керування цикл. зрушенням блоку за законом ключа

Шифр монопідстановки – задається ключем у виді входу і виходу. У рядку вхід записується вихідний алфавіт. У рядку вихід записується одна з можливих комбінацій (символи алфавіту в довільному порядку).

Вхід:    а   б   в   г....

Вихід: я   д   щ  з …...

Найважливішою характеристикою всіх розглянутих шифрів є кількість вихідних  ключів, що дозволені в системі.

На рис.5.2 приведений алгоритм блокового симетричного шифрування (чи складеного шифру).

Рис.5.2

Лекція 6

Алгоритми і засоби формування ключів і паролів.

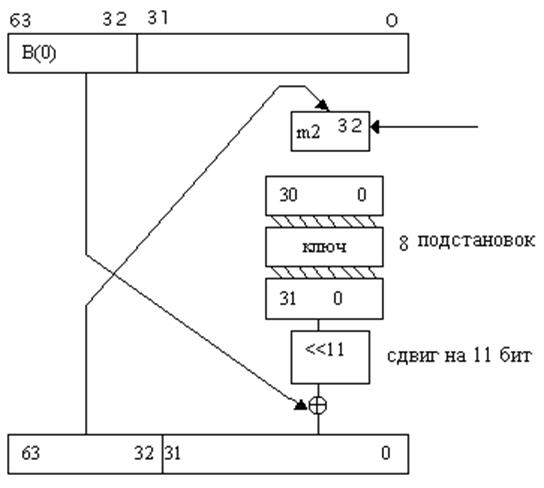1.  Вимоги.

2.  Лінійний рекурентний регістр. Його властивості.

3.  Лінійний конгруентний генератор.

4.  Проблемні питання.

 Обчислювально стійкі системи реалізуються на основі використання вихідних ключів визначеної довжини, тоді:

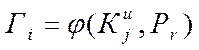                                                                                (1)

                                                                                  

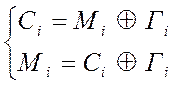
У реалізації системи шифрування (2), (3) найбільш складною задачею є формування Гi, що задовольняє наступним умовам:

1. 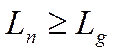                                                                                          (4)

Lg – min припустиме значення.

2. Гi повинна володіти високою структурною скритністю.

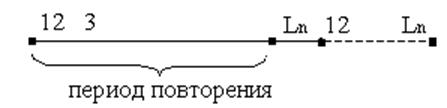                                                                    Рис.6.1

       структурна скритність - 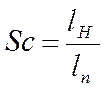                                               (5)

lн – мінімальна кількість біт з послідовності, при знанні яких можна визначити закон формування послідовності  φ.

Кращий випадок, якщо  (якщо ) – називається абсолютно (зовсім) потайливий. Це може бути тільки  фізичний випадковий  процес. У житті за рахунок перетворення ? можна досягти тільки кінцевих значень структурної скритності.