4) lo- відстань одиничності КС.
tб – математичне чекання часу розкриття КС із використанням конкретного методу. Найбільше простій – метод підбора чи грубої сили, тоді якщо потрібно перебрати N – варіантів, то
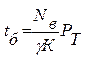
![]()
![]() -
імовірність, з яким необхідно здійснити криптоаналіз.
-
імовірність, з яким необхідно здійснити криптоаналіз.
g - продуктивність КАС, зміна кількості можливих переборів за секунду.
![]() сек/рік.
сек/рік.
У граничному випадку Nв = Nк, де Nк – N ключів.
Т.3.1.
Необхідною і достатньою умовою теоретичної недешифруемості чи безумовної стійкості є умова:
![]() , тобто імовірність появи (8)
, тобто імовірність появи (8)
Криптограма в системі не повинна залежати від того, яке повідомлення обране. Фізично це означає, що будь-яке повідомлення може відбитися в будь-яку криптограму з рівною імовірністю.
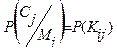 (9)
(9)
Доказ: визначимо імовірність 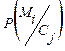 , що може обчислити КРА .
, що може обчислити КРА .
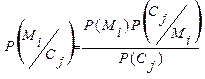 (10)
(10)
Якщо 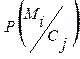 =Р(Mi)
– КРА не одержав ніякої інформації про Сj.
=Р(Mi)
– КРА не одержав ніякої інформації про Сj.
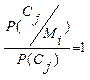 (11)
(11)
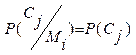 Відомо дві системи, що
забезпечують безумовну стійкість: система Вернама і система «гаряча
лінія».
Відомо дві системи, що
забезпечують безумовну стійкість: система Вернама і система «гаряча
лінія».
У системі здійснюється потокове шифрування, тобто символи криптограми в шифраторі шифруються за правилом:
![]() (12)
(12)
Мi – i- тий символ, ![]()
Результат – символи ключа.
Відмінною рисою є те, що символи ключа Кi породжуються випадковою порівняно ймовірностною послідовністю, випадковим процесом. У такій системі в символів (довжина ключа) повинне бути не менш довжини повідомлення.
![]() (13)
(13)
![]() (14)
(14)
Сi – символи криптограми.
Кi – символи ключа.
m – підстава алфавіту.
Аналіз (12) і (14) показує, що для зашифрування і розшифрування потрібно використовувати ту саму випадкову послідовність (ключ).
Можна показати, що для цієї системи умовна
ентропія ![]() :
:
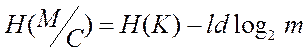 (15)
(15)
l – довжина ключа.
d – надмірність алфавіту.
Визначимо умову, при якому реалізується безумовна стійкість, тобто знайдемо в символів криптограми, при якому не можна здійснювати криптоаналіз.
Задача криптоаналізу може бути визначена коли:
![]()
![]()
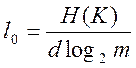 (16)
(16)
Фізично l0 – мінімальна кількість символів криптограми при правильному одержанні яких можна сподіватися на успішний криптоаналіз. Якщо l< l0,то система безумовно стійка. Це друга умова реалізації безумовно стійкою системи.
1. Відстань одиничності для безумовно стійких (БС) і обчислювально стійких(ВР) КС.
2. Умова реалізації ВР КС.
3. Приклади.
Ціль: виявити умова реалізації ВР і БС КРС для моделі, приведеної на рис.3.1.
Задача оцінки відстані одиничності: КРА послідовно перехоплює криптограми З1,…Сn і вирішує задачу визначення значеннєвого змісту переданого Мi – повідомлення і ,як найбільш важливу, задачу визначення ключів Кj.
Очевидно, що
його успіх у рішенні задач залежить від обсягу криптограм, що він одержав, при
цьому КРА знаходиться в невизначеності ![]() .
.
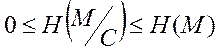 (1)
(1)
Найкращий
випадок, якщо ![]() .
.
По Шенону:
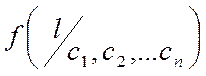 (2)
(2)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.