Информатика и выч. техника \ Основы теории защиты информации

Основи теорії захисту інформації: Конспекти лекцій № 1-32 (Введення в криптологію, основні поняття і визначення. Проблеми теорії і практики криптології), страница 38

1) Характеристика проблематики.

Для RSA 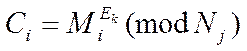                                                                           (1)

Для Ель- Гамаля

Проблематика цих питань :                                                                                     (2)

Складність : (1) – прості цілі числа .. Стандартна машина , арифметика m=32, 2.

Задача полягає у тому, щоб обчисляти великі прості числа використовуя стандартну машинну арифметику.

2) Аналіз складності операції множення

Операції модульні, потрібно ділити весь час на модуль - це дуже складно.

Над простим полем

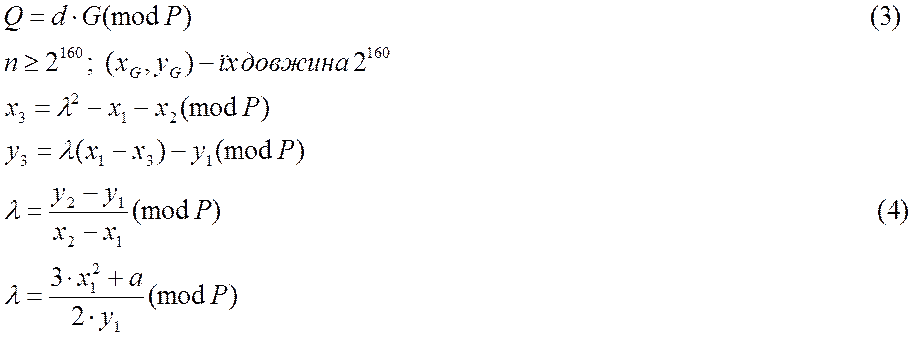             - основна проблема – це ділення.

Нехай ми застосовуємо просте множення в таблиці

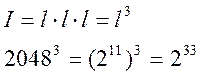
3) Аналіз складності піднесення до ступеня

Методи піднесення до ступеня:

1. Зліва направо

2. Зправа наліво

3. Блоковий з постійною довжиною блока

4. Блоковий з перемінною довжиною блока

Двійковий бінарний зліва направо

Сутність:                                                                                                                   (5)

Представимо n у вигляді . Якщо у двіцковому методі буде “1”, то ми запишемо послідовно КМ, якщо ”0”, то запишемо К.

К – означає піднесення  поточного значення до квадрата.

М – множення на х.

В логічному представлені (КМ, К) найстаршим завжди буде КМ, він викреслюється, а далі за мінімальний час здійснюється піднесення до ступеня.

Приклад 1.

За мінімальну кількість кроків обрахувати .

Якщо виконувати послідовне множення, то їх буде 39. n=39, n=”100111” – двійкрвий вид числа. Зробимо заміну

N=KM, K, K, KM, KM, KM.

Потім розраховуємо перше , друге , далі , слідуюче , далі.

Маємо

5 – операцій зведення у квадрат;

3 – операції множення.

Приклад 2.

КМ, КМ, КМ, КМ, КМ, К, КМ, К, К, К.

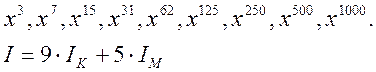
Основним недоліком є те, що складність піднесення до ступеня залежить від ччисел 0 и 1.

Блоковий метод з однаковими блоками

 - базується наm-ічном представлені числа

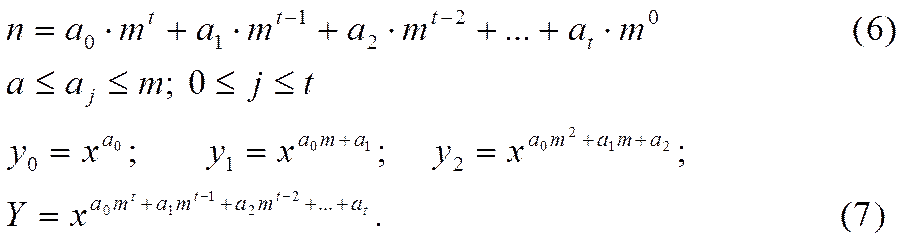
Якщо m=2, то наша формула як і двійковий бінарний метод.

Особливості:

Можно спочатку обчислити , потім їх можно використовувати.

2. Блоковий метод з нерівномірною довжиною блока

Сутність методу:

Z=XY(mod N)

Нехай є число Y у вигляді блоків , где-довжина блоку, з довжиною відповідно .

Введемо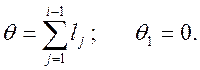

.

Метод з перемінною довжиною блока має переваги:

1.Складність методу практично не залежить від кількості “1” і “0” (в 10 раз менш ніж для двійкового методу).

2.В 1.7 раз зменшується складність, тобто збільшується швидкість піднесення до ступеня.

Недолік:

Треба розраховувати таблицю.

3)Множення

При виконанні операцій множення можна користуватися методом множення в стовбчик, і цей метод потребує l2 операцій “+”.

Метод Монтгомері.

Нехай є Х, l-довжина Х, операції виконуються по . Тоді існує для Х взаємнообнозначне відображення в просторі Монтгомері:

                                                                                                               (9)

де R=.

M(X)-числа Монтгомері. Операція “” зводиться до зсуву і “+” по .

Обернене перетворення:

                                                                                           (10)

де R-1=.

Сутність застосування:

1.Метод вимагає попереднього відображення  і закінчене відображення . Операція ефектевна, якщо здійснювати піднесення до ступеня, тоді спочатку Х перетворюється в число Монтгомері, далі здійснюється піднесення до ступеня (тобто багатократне множення), в кінці результат перетворюється за допомогою оберненого перетворення.

Лекція  32

ПРОБЛЕМИ ТЕОРІЇ І ПРАКТИКИ КРИПТОЛОГІЇ

1.Поняття стенографії та її застосування.

2.Квантова криптографія.

3.Осносні проблеми криптологіїта можливий їх розв’язок.

1)Поняття стенографії та її застосування

Під стеганографією розуміється спосіб тайнопису, який більш давніший ніж сама криптографія. Основною метою криптографії є забезпечення конфеденціальності, цілосності, спостереженності та доступності за рахунок використання методів криптографічного захисту інформації (КЗІ). На відміну від криптографії, метою стеганографії є також забезпечення конфеденціальності, цілосності, спостереженності та доступності, але за рахунок використання тиких методів:

Скачать файл