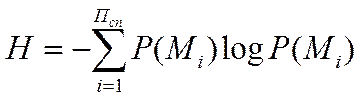 (6)
(6)
Mi з метою забезпечення їх Ц, П автентифіцируються в
пристрої 2 за законом ключа ![]() . В результаті на виході
формується
. В результаті на виході
формується 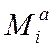 .
.
Шифратор 3 здійснює зашифрування за правилом (2), у результаті на виході шифратора формується виробництво криптограм Сj і будемо думати відомої апріорну статистику появи криптограм на виході шифратора - Р(Сj).
Думаючи, що відомо імовірність:
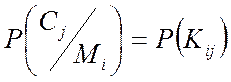 (7)
(7)
Фізичний зміст – за законом ключа Кj зашифрування.
Повідомлення Mi відображається в криптограму Сj і це дорівнює застосуванню Кij.
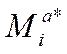 .
.В ПА здійснюється обчислення відкритого
підпису за законом ключа 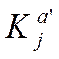 .
.
У результаті на виході 10 формується
повідомлення 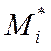 , цифровий підпис відрізається. Користувач
одержує повідомлення.
, цифровий підпис відрізається. Користувач
одержує повідомлення.
Примітка:
Для працездатності системи П1, П2 повинні мати
погоджені пари ключів, для автентифікації - (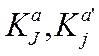 ), для
шифрування - (
), для
шифрування - (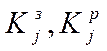 ). Ці функції виконує джерело
ключів із ключовими пристроями.
). Ці функції виконує джерело
ключів із ключовими пристроями.
Якщо 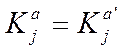 , система
називається симетричної, якщо
, система
називається симетричної, якщо 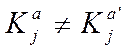 , система називається
несиметричної.
, система називається
несиметричної.
1. Математична модель КРС.
2. Умови реалізації БСС.
3. Відстань рівнозначності.
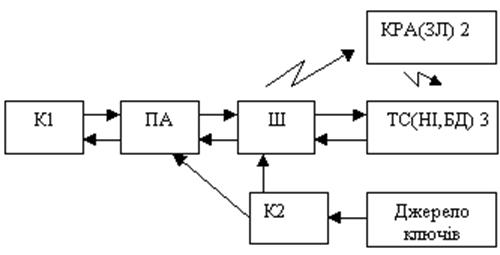
На рис. 3.1. приведена спрощена схема забезпечення криптографічного захисту повідомлень.
 |
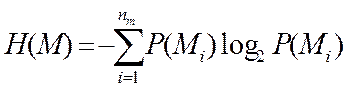 (1)
(1)
Рис.3.1.
Користувач К1 – джерело інформаційних
повідомлень Mi, розмір джерела (кількість повідомлень) ![]() .
Розмір ймовірність появлення повідомлення Р(Mi) апріорна ентропія Н(Mi) джерела
інформації. З метою забезпечення цілісності і дійсності повідомлення Mi
піддається криптоперетворенню – автентифікації, на виході формується Mi.
.
Розмір ймовірність появлення повідомлення Р(Mi) апріорна ентропія Н(Mi) джерела
інформації. З метою забезпечення цілісності і дійсності повідомлення Mi
піддається криптоперетворенню – автентифікації, на виході формується Mi.
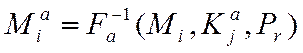 (2)
(2)
Кj – ключ, обираний із простору ключів,
розмірність 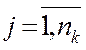 .
.
Для забезпечення конфіденційності, ![]() - повідомлення 2 піддається шифруванню, на
виході формується Сj – криптограма.
- повідомлення 2 піддається шифруванню, на
виході формується Сj – криптограма.
![]() (3)
(3)
Сj передається К2 через ТС по відкритому каналі, чи записується на носій інформації.
КРА – зовнішня сторона, не входить у систему.
Думаючи, що КРА знає Р(Mi) - апріорну статистику й ентропію Н(Mi), ставить
задачу визначити яке повідомлення міститься в Сj і який ключ використовується
для зашифрування Кj, і який ключ ![]() використовується для
автентифікації.
використовується для
автентифікації.
Думаючи, що КРА відомо апріорну статистику:
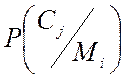 ,
, ![]()
Імовірність постановки задачі визначаємо імовірність того, що в Сj міститься Мj.
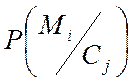 - умовна апостеріорна імовірність.
- умовна апостеріорна імовірність.
КРА використовуючи 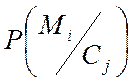 може знайти умовну
ентропію
може знайти умовну
ентропію ![]() .
.
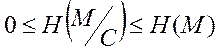 (4)
(4)
У процесі нагромадження криптограм КРА зменшує свою невизначеність, у результаті деяка інформація ΔI, яку можна вимірити:
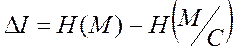 (5)
(5)
Умовна імовірність 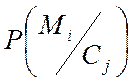 можна
визначити використовуючи теорему:
можна
визначити використовуючи теорему:
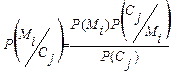 (6)
(6)
Реально, можна побудувати КС із 4 рівнями стійкості:
1. Безумовно стійкі КС чи теоретично не дешифруємі.
2. Обчислювально стійкі чи гарантован стійкі.
3. Ймовірно стійкі чи доказово стійкі.
4. Обчислювально не стійкі чи тимчасово стійкі.
Для класифікації можна використовувати різні показники і критерії. Найбільш кращим є використання наступних характеристик:
1) Nk – обсяг ключів.
2) H(k) – ентропія джерела ключів:
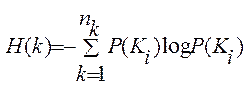 (7)
(7)
![]() - імовірність появи Кj
– ключа в системі.
- імовірність появи Кj
– ключа в системі.
3) tб – безпечний час.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.