P=2R+1 (15)
Р – просте
Зловмиснику
доступний відкритий ключ ![]() , він знає N, тоді він
може знайти
, він знає N, тоді він
може знайти ![]() , якщо він довідається
, якщо він довідається ![]() , тобто P і Q. Основна його задача
розкласти N на 2 співмножники P і Q. Ця задача називається факторізациею
модуля.
, тобто P і Q. Основна його задача
розкласти N на 2 співмножники P і Q. Ця задача називається факторізациею
модуля.
RSA – доказово стійка система, тому що доказ стійкості зводиться до доказу складності розкладання N на 2 співмножники.
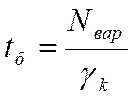
За останні 20 років математика працювала над рішенням задачі факторизації дуже великих чисел.
Теорії:
1. Теорія Р-1, ?
2. Теорія Ленстри
3. Двійкове решето
4. Загальне решето числового поля
Для 4 –случаю
складність криптоаналізу оцінюється з використанням суб експоненціального алгоритму:
![]() (16)
(16)
?, ? – параметри методу
δ=1,96 ν=1/3
І – кількість групових операцій, який треба виконати для факторизації методу N.
(частина 2)
1. Загальна характеристика.
2. Схеми розподілу ключів по відкритих каналах.
3. Оцінка стійкості.
4. Проблеми теорії і практики.
![]() (1)
(1)
Відняти один з іншого складно.
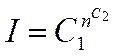 (2)
(2)
n – розмірність вхідних даних, для RSA – N – довжина модуля перетворення в бітах.
При спрямованому шифруванні параметри і ключі поділяють на 2 групи:
1.
особисті ![]()
2.
публічні (відкриті) (![]() ),
), ![]()
k – ий користувач генерує особисті і відкриті ключі і параметри.
ν – ий користувач
шифрує ![]() використовуючи:
використовуючи:
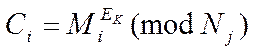 (3)
(3)
розшифрувати її може k – ий користувач, тоді:
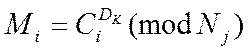 (4)
(4)
Для спрямованого шифрування:
1.
Найбільш оптимальним
методом для криптоаналізу є перехоплення повідомлення ![]() .
.
2.
Факторизація модуля ![]() (знайти P, Q).
(знайти P, Q).
3. Потім знайти
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
δ, ν – параметри, залежать від методу факторизації.
Мається n – користувачів мережі, кожний з них генерує ключі своєї станції, частина з них може оголосити особистими чи конфіденційними, а частина може роздати користувачам мережі.
Треба
виробити ключ зв'язку (захисту) інформації на сеанс, скориставшись відкритими
каналами зв'язку. Наприклад: виробити ![]() , у тому
числі для симетричної системи. Зважується в полях Галуа.
, у тому
числі для симетричної системи. Зважується в полях Галуа.
Протокол, що одержав поширення вироблення загального секрету 2 користувачами – протокол Діфі – Хелмана.
Нехай маються користувачі А и В, один з них чи центр генерує пари чисел P, Θ.
P – просте число.
Θ – первісний елемент, що породжує поле GF(p).
![]()
![]()
![]()
Θ – просте число, з інтервалу 0, Р-1, що будучи зведене в ступінь дає структуру простого поля, тобто з'являться всі числа один раз.
![]()
Кожен користувач генерує ключі Х с довжиною l.

Після цього обчислюють відкритий ключ:
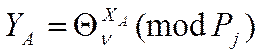
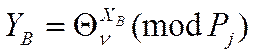 (8)
(8)
Після цього розсилають відкриті ключі по відкритих каналах один одному, забезпечуючи при цьому їх цілісність і дійсність. Кожний з них може обчислити загальний секрет:
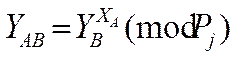
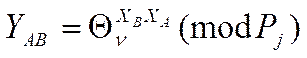
![]() (9)
(9)
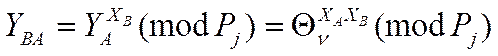 (10)
(10)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.