![]() (11)
(11)
Значить загальний секрет може бути використаний як ключ симетричного шифру. Стійкість цієї схеми:
Основна задача КРА – знайти ХА, ХВ. Простіше всього угадування ХА, ХВ, захиститися від цього можна вибравши велику довжину ключа і виробити їх випадково.
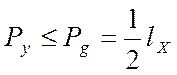
Т.к. ![]() - відкриті параметри, те КРА знаючи їх
може спробувати вирішити рівняння:
- відкриті параметри, те КРА знаючи їх
може спробувати вирішити рівняння:
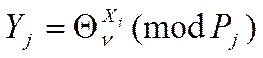
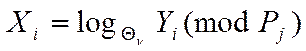 (12)
(12)
(12) – проблема дискретного логарифма (дискретне логарифмічне рівняння - ДЛР).
Стійкість схеми Диффи – Хелмана визначається складністю рішення дискретного логарифмічного рівняння виду (12).
Для методу розрахунку загального числового поля складність рішення носить субекспоненціальний характер і може бути оцінена співвідношенням (7) зі своїми параметрами ?, ?.
Є ряд загальних проблем реалізації і застосування цих алгоритмів.
1. Проблема генерації великих простих чисел відповідної довжини.
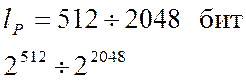
2. Складність обчислень.
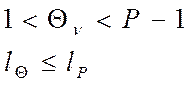
3. Арифметична багаторазова точність. Складність цих перетворень дуже велика, набагато більше, ніж у симетричних криптосистемах.
4.
![]()
Застосування методів RSA і Діфі – Хелмана привело до появи нових математичних методів криптоаналізу:
- методи факторизації
![]()
- задача рішення ДЛУ:
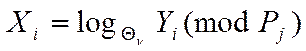
для (1) метод Поларда (Р-1 і ρ), методи Ленстрі, двійкове решето, загальне і спеціальне решето числового поля.
Протиріччя дозволяється за рахунок збільшення ![]() , але збільшується складність обчислення
відкритого ключа, зменшується швидкість шифрування. Протиріччя дозволяється за
рахунок виконання рівнобіжних перетворень у групах точок еліптичних кривих над
полями.
, але збільшується складність обчислення
відкритого ключа, зменшується швидкість шифрування. Протиріччя дозволяється за
рахунок виконання рівнобіжних перетворень у групах точок еліптичних кривих над
полями.
Лекція 8
Криптоперетворення в групах точок еліптичних кривих
1. Поняття еліптичної кривої над полем Галуа.
2. Метрика операцій на ЕК.
3. Приклади.
Складність перетворень у ЕК:
![]() (1)
(1)
де n – порядок базової точки на ЕК (період).
Ця складність набагато більше, ніж субекспоненціальна
складність від ![]() .
.
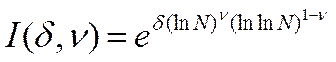 (2)
(2)
![]()
![]()
Кубічна ЕК в афінном базисі над простим полем має вид:
![]() (3)
(3)
![]() - точки ЕК,
- точки ЕК,
а, б – параметри ЕК
![]() (4)
(4)
![]() - належить ЕК, якщо ця
пара чисел задовольняє порівнянню (3). Над розширеним полем
- належить ЕК, якщо ця
пара чисел задовольняє порівнянню (3). Над розширеним полем ![]() рівняння ЕК має вид:
рівняння ЕК має вид:
![]() (5)
(5)
![]() - точка на ЕК,
- точка на ЕК,
а, б – коефіцієнти (параметри) ЕК
f(x) – примітивний поліном над полем ![]() .
.
![]() (6)
(6)
Поліном називається примітивним, якщо він що не
приводиться, а з іншої сторони породжує поле ![]() .
.
У рівнянні (5) ![]() , а
також а і b являють собою m-бітні вектора в
поліноміальному чи нормальному базисах, зокрема, у поліноміальному базисі x, y,
a, b, є поліномами не вище m -ступеня, тому всі операції виконуються не вище m
– ступеня.
, а
також а і b являють собою m-бітні вектора в
поліноміальному чи нормальному базисах, зокрема, у поліноміальному базисі x, y,
a, b, є поліномами не вище m -ступеня, тому всі операції виконуються не вище m
– ступеня.
Є 3 – мірне перетворення ЕК, називається проективною геометрією (представлення). У проективній геометрії кожна точка задається - X,Y,Z – дозволяє прискорити проведення операцій.
![]() (7)
(7)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.