![]()
![]() (19)
(19)
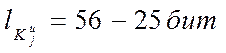
![]() (20)
(20)
Пристрій чи
алгоритм, що формує Гi, тобто реалізує функцію j, називається шифратором, необхідний ключ довжини 100
– 1000 біт 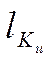 .
.
Для такої системи Гi повинна задовольняти ряду вимог:
1)
мати свідомо заданий
період (![]() ),
), ![]() і
більш,
і
більш, ![]() символів.
символів.
2)
![]() повинна
мати складний закон формування ключа, інакше погана структурна скритність.
повинна
мати складний закон формування ключа, інакше погана структурна скритність.
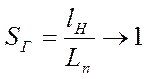 (21)
(21)
![]()
![]() - повний період.
- повний період.
3) відновлюваність Г, простору і часу.
4) однозначність формування Г i мінімальна складність функції j.
1. Класифікація і характеристика.
2. Афіні шифри.
3. Потокові шифри.
4. Блокові і складені шифри.
Застосовувані на практиці криптоперетворення розділяють на 2 класи по стійкості:
1. обчислювально стійкі.
2. ймовірно стійкі (доказово стійкі).
Основним показником, по якому оцінюються такого роду системи є безпечний час:
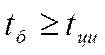 (1)
(1)
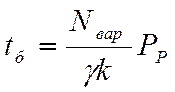 (2)
(2)
Nвар – кількість команд, операцій для рішення задачі криптоаналізу.
g - продуктивність криптосистеми, вар/сек.
RSA: N=P*Q (3)
k –
коефіцієнт кількості сек/рік ![]()
Рр – імовірність рішення задачі.
![]() (4)
(4)
x-?
ВР і ДС повинні задовольняти (1). До доказово стійких перетворень відносять перетворення з відкритими ключами, з відкритим поширенням ключів і т.д. У цих системах задача криптоаналізу полягає в рішенні якоїсь іншої математичної задачі. Обчислювально стійкі системи реалізуються за рахунок застосування симетричних криптоперетворень.
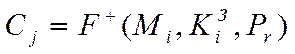 (5)
(5)
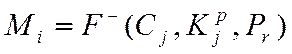 (6)
(6)
У симетричних криптосистемах ключ зашифрування або збігається з ключем розшифрування, або обчислюється один з іншого з поліноміальною складністю.
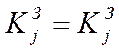 (7)
(7)
Нехай n – розмірність вхідних даних, що підлягають криптоперетворенню і нехай t(n) є складність перетворення цих даних у сек. тактах, командах. Складність називають поліноміальної, якщо вона представлена:
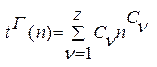 (8)
(8)
![]() - набір констант.
- набір констант.
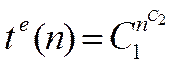 - експонентна складність
(9)
- експонентна складність
(9)
В даний час як функцію f реалізуючої криптоперетворення використовуються афінні шифри.
Афінне перетворення – перетворення, яке можна одержати комбінуючи рухи, дзеркальні відображення і гомотепію в напрямку координатних осей.
Гомотепія – перетворення простору чи площини щодо точки по направляючим осях з коефіцієнтами.
До афінних шифрів відносяться чи шифри перетворення зрушення, лінійні шифри, афінних шифри. Нехай Мi – символ чи повідомлення цифри (буква), нехай також а і s ключі, причому:
![]()
![]()
НСД(a, n)=1
то існує оборотний афінний шифр із функцією зашифрування:
![]() (10)
(10)
n – модуль перетворення шифру, розмір алфавіту.
i - функція перетворення.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.