Що перевіряється m поділяється послідовно на всі
прості числа менше ![]() .
.
![]() (1)
(1)
Якщо m не поділяється на всі ![]() ,
то воно просте, тобто:
,
то воно просте, тобто:
m = p
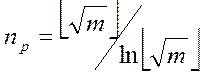
Цей метод рекомендується для коротких довжин, чи як додатковий метод. Прості числа повинні закінчуватися 1, 3, 7, 9.
![]()
Де k-просте, простими є 2,3,5,7,11,13,17,19,31,107,127,607,…19997і т.д.
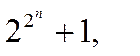
![]() для таких n- просте.
для таких n- просте.
Для числа m, для якого відомо канонічне розкладання m-1 справедливе теорема Люка:
Якщо для (а, m) ![]() , то
m-просте.
, то
m-просте.
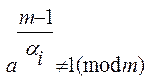
![]()
Перший метод базується на теоремі Ферма.
![]()
![]()
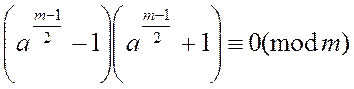
Тест Лемана
1) 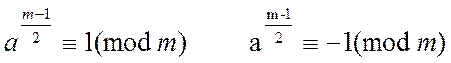 (2)
(2)
Якщо а – первісний елемент, то ![]() генерується
t-чисел а, взаємнопростих з m, потім для кожного а здійснюється перевірка.
генерується
t-чисел а, взаємнопростих з m, потім для кожного а здійснюється перевірка.
2) Якщо на всіх t – перевірках одне з умов
виконується, те число m можна вважати псевдопростим, це число з імовірністю ![]() того, що число не просте.
того, що число не просте.
Примітивні поліноми табульовані і відомі усі до 2000 ступеня.
Метод гіпотез не застосовується, тому що базується на недоведених гіпотезах.
Базовою точкою на ЕК може вважатися кожна ![]() - точка, що з однієї сторони задовольняє
рівнянню ЕК, а з іншої має порядок n.
- точка, що з однієї сторони задовольняє
рівнянню ЕК, а з іншої має порядок n.
![]() , n- просте
, n- просте
G – повинна бути випадкової.
![]() nh=И
h-k – фактор=2,4,8
nh=И
h-k – фактор=2,4,8
Найбільш складна задача побудови ЕКіз заданими значеннями И =nh. Треба знайти параметри (a, b, q), а також n, И, зв'язані
4) (a, b, q, n, И) – випадкові.
Відомо 3 методи побудови:
1. метод комплексного множення
2. метод Скуффа
3. метод через підполя
Окремий випадок, якщо ![]() . Якщо m
розкладається на співмножники,
. Якщо m
розкладається на співмножники,
![]()
![]()
![]() за методикою
перерахувати для випадку m.
за методикою
перерахувати для випадку m.
1. Метрика додавання і подвоєння в проективних координатах.
2. Тест Рабінера – Міллера побудови простих чисел.
3. Приклади розшифрування в розширених полях.
Рівняння кривої в проективних координатах
![]() (1)
(1)
Можна показати, що операції додавання і подвоєння для кривої (1) можуть бути обчислені в наступному виді:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
______________________________________________________________
![]()
![]()
![]()
![]()
![]()
![]()
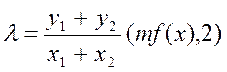
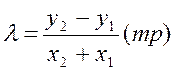
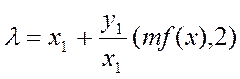 (2)
(2)
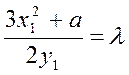
![]() (3)
(3)
![]()
![]() (4)
(4)
Рішення (4) вимагає значних ресурсів, алгоритму Евкліда.
m ³160
У проективних координатах немає розподілу по суті.
![]()
Завжди буде однозначність відображення з афінних координат у проективні і навпаки.
![]()
![]() (5)
(5)
Імовірність, що число просте не перевищує ![]() .
.
Числа Кармайкла ("брудні поросята")
561, 3, 11, 17
Вони проходять цей тест. Чим більше t, тим менше імовірність проходження в тесті.
Тест Соловея – Штрассена.
Базується на t – іспитах, генерується t – раз.
1) ![]() , причому
, причому ![]() ,
, ![]() генерується
t -раз.
генерується
t -раз.
2) перевіряється НСД, ![]() , те
число складене.
, те
число складене.
3) знаходиться символ Якобі
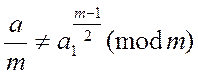 - число складене (6)
- число складене (6)
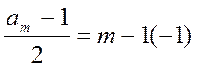
Р=7 1 2 4 1 2 4 1
а=3 i | 0 1 2 3 4 5 6 Справедливо (5).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.