Основи теорії захисту інформації: Конспекти лекцій № 1-32 (Введення в криптологію, основні поняття і визначення. Проблеми теорії і практики криптології), страница 14

                 ai  | 1  3  2  6  4  5  1

Тест Рабінера - Міллера

Нехай m – непарне, просте, представимо:

                                                                                           (7)

m,  s   - не пара

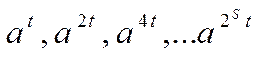                                                                       (9)

З обліком (7) випливає:

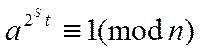                                                                                 (8)

У ряді (9) кожен попередній елемент є корінь з наступного елемента.

 - елементи поля, , , то ряд (9) складається з одиниць, перед якими може випливати  -1, чи

                                                                                       (10)

чи для всіх  0 £ j £ s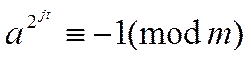      

Число m, що задовольняє хоча б одній умові, називається сильним псевдопростим у змісті Рабінера – Міллера.

Якщо проводити t– іспитів, то імовірність того, що в кожнім іспиті не буде виявлене просте число не перевищує ¼.

На t – іспитах  

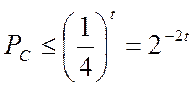                                                                                (11)

Порівнюючи з (5) бачимо, що збіжність тесту Рабінера – Міллера набагато вище.

Алгоритм перевірки

1. 

2.  НСД ¹1   m – складене

3.     

4.  якщо        m – можливо просте

5.     доти поки

6.  якщо  , те m – складене

якщо , m – можливо просте

                                                                 

Проводимо t1 – експериментів, після цього підтверджуємо (11).

                                                              

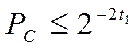
1.  Знайти

2.  Добуток і сума

                                                      

3. 

                                                           

Лекція 11

Принципи реалізації спрямованого шифрування

1.  Спрямоване шифрування в кільцях і полях.

2.  Методи спрямованого шифрування в групах точок ЕК.

3.  Обговорення результатів.

Сутність спрямованого шифрування в  RSA - алгоритмі.

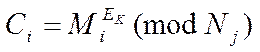                                                                       (1)

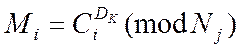                                                                          (2)

                                                  

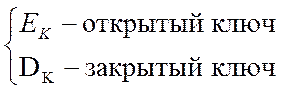
                                       -  випадкова пара

Якщо пари  генерується k– им користувачем, то він може записати на носій у захищеному виді і зберегти його в таємниці.  перетвориться в сертифікат і розсилається усім внутрішнім користувачам. У цьому випадку всі користувачі володіють . Можуть здійснювати спрямоване шифрування за правилом (1). Розшифрувати  - криптограму може тільки k - ий користувач, що володіє - ключем. Такий несиметричний шифр називається спрямованим шифром.

Недоліки RSA спрямованого шифру

Доказова стійкість, її доказ зводиться до факторизації . Розвиток математичних методів і криптоперетворень приводить до зменшення складності факторизації.

Сутність перетворення Ель – Гамаля

1 етап: являє собою реалізацію розподілу ключів по відкритих каналах зв'язку. Усі користувачі одержують загальносистемні параметри , де Р – просте, Q - первісний елемент (у всіх користувачів вони однакові). Кожен користувач генерує особистий ключ , що являє собою випадкову послідовність (х  не менше 160 біт). Потім х – компоненти з'являються особистими ключами і зберігаються в таємниці. Після цього кожен користувач обчислює відкриті ключі. Потім відкриті ключі поширюються в мережі з забезпеченням цілісності і дійсності.

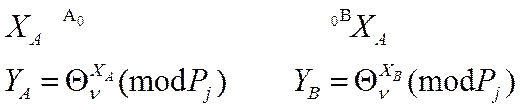                                                                                                             (3)

2 етап: ключ спрямованого шифрування

                                                                             (4)

К – сеансовий ключ, випадкове число.

(k,p-1) = 1

Нехай необхідно зашифрувати - ий блок. Далі обчислюються компоненти:

                                                                                 (5)

і сеансовий відкритий ключ, після обчислюється відкрита криптограма:

                                                                    (6)

Передачі підлягає  щораз. Операція групова.