Основи теорії захисту інформації: Конспекти лекцій № 1-32 (Введення в криптологію, основні поняття і визначення. Проблеми теорії і практики криптології), страница 21

                                           (1)

     - коефіцієнти багаточлена над GF(q).

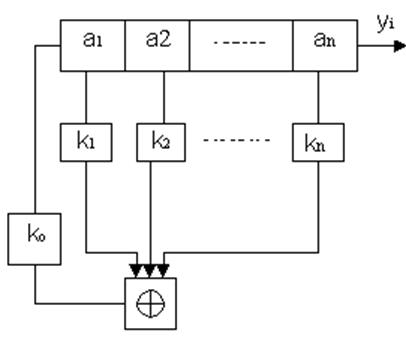
Нехай необхідно побудувати ЛРР, що виробляє двоїчну ЛРПМП довжиною , робота якого визначається (1).

                                     Рис.16.1 - Структурна схема цього регістра

 - визначає поточне (початкове) стан.

  - визначає необхідні зворотні зв'язки.

При подачі на ЛРР такту частоти регістр входить у робочий стан. На кожному i - тому такті вміст останнього регістру  зчитується на вихід , тим самим доповнюючи ЛРПМП наступним символом. У той же час значення всіх регістрів збільшується на відповідні коефіцієнти k і надходять на вхід загального суматора. Результат підсумовування збільшується на kо і надходить на вхід регістра. На цьому робота ЛРР на черговому такті завершується. Т.к. ЛРР має період , те після тактів роботи регістр приймає вихідне значення.

У нашому випадку необхідно одержати двійкову послідовність, тому вектор  є двійковим а в суматорі є сума (mod 2). Для розкриття формування закону ЛРПМП необхідно перехопити 2l – символів безпомилково, тобто якщо l =257 то 2*257=514біт.

Розглянемо правила перетворення в поле Галуа:

                                                   

                                                 (2)

 - елементи формованої послідовності.

 - первісний елемент полючи Галуа.

 - проміжні модулі.

 m – основа алфавіту.

У (2) повинне виконуватися умови:

                                             (3)

Pn- довільна основа алфавіту символів формованої послідовності. Застосування (2) дозволяє з однієї сторони істотно підвищити кодову стійкість, тобтостійкість проти визначення закону формування псевдовипадкової послідовності, з іншої сторони дозволяє будувати послідовність з необхідною підставою алфавіту. Було здійснено всебічне тестування формування послідовностей з використанням статичних тестів (використовуючи критерій Пірсона  , визначення Холмогорова). Дані дозволили сказати, що використовуючи вираження (2) можна будувати m- ічні ПСП якого завгодно великого періоду, при цьому також теоретично обґрунтоване, що m - ічні символи формованої послідовності з'являються також порівняно ймовірно і незалежно.

Тестування джерел випадкових і ПС чисел на основі методики стандарту США  FIPS-140-1

Стандарт FIPS-140-1 визначає 4 статичних тести на випадковість:

-  монобітний

-  блоковий

-  тест серій

-  тест довжин серій

Для них задаються границі для задовільних значень, статичних параметрів. Окремий бітовий рядок довжиною 20 000 бітів піддається кожному з 4 приведених тестів.

Монобітний тест

 Суть тесту в підрахунку кількості 0 і 1 на відрізку послідовності визначеної довжини.

                                                         

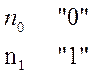
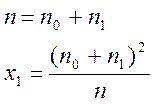
Послідовність а довжиною n, параметр х, підкоряється закону розподілу  з одним ступенем волі і цей тест може застосовуватися за умови, що n >10, якщо послідовність випадкова, те:

                                                      

Блоковий тест (Покеру)

Нехай послідовність має довжину n, хочемо перевірити появи блоків довжиною m.

                                                    

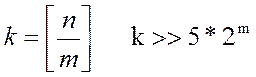
Поділимо послідовність а, довжини n на k – неперекриваючихся частин, підрахуємо частоту появи різних блоків довжиною m.

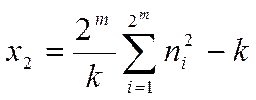                                                                       (4)

Методика перевірки полягає в тім, що спочатку розраховується експериментальне значення, а потім розраховуються граничні, додаткові значення і хi порівнюється з х граничним, якщо ,  те гіпотеза відкидається.

Статичний параметр, заданий рівнянням обчислюється для m = 4 і статистика повинна задовольняти умові:

                                                            

Тест серій

Під серією розуміється послідовність однакових символів, 1 чи 0. Суть тесту: на заданій довжині тестуємої поверхні здійснюється підрахунок серій довжиною 1, 2, 3, 4,  5, 6 елементів. Серії більш 6 розглядаються як 6.

Якщо послідовність випадкова, то кількість серій: