![]() (9)
(9)
На основі аналізу складових ЦП знаходиться цілісність та достовірність,
у тому числі підписана інформація ![]() має вид:
має вид:
![]() (10)
(10)
Якщо порівняння (10) виконується, то повідомлення вважається цілісним та достовірним з деякою ймовірністю.
Стійкість залежить від факторизації ![]() .
(11)
.
(11)
У класі перетворень Ель - Гамаля система ЦП здійснюється за два етапи:
1. здійснюється генерація та розподілення ключів, тобто кожен користувач, генерує собі ключ, зберігає його в собі в таємниці, а відкритий ключ обчислює як:
![]() (12)
(12)
Відкритий ключ розповсюджує всім кореспондентам системи.
2. на цьому етапі Ель - Гамаль запропонував сформувати підпис як дві
компоненти ЦП: ![]() .
.
Ці компоненти формуються на основі розв'язку класичного порівняння Ель - Гамаля:
![]() (13)
(13)
де ![]() - первісний елемент у полі,
- первісний елемент у полі, ![]() - хеш - функція,
- хеш - функція, ![]() -
відкритий ключ.
-
відкритий ключ.
![]() (14)
(14)
![]() (15)
(15)
Підставимо (12) та (15) у (13):
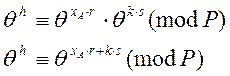
![]()
![]() (18)
(18)
(18) є фундаментальним виразом, бо дозволяє обчислити другу компоненту
ЦП, а саме ![]() :
:
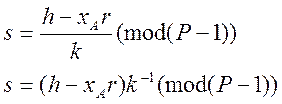
![]()
Перевірка: здійснюється всіма користувачами, які володіють відкритим ключем та загальносистемними параметрами. Здійснюється на основі перевірки порівняння (13).
Стійкість перетворення визначається складністю розв'язку порівняння (12).
Лекція № 16
Методи та алгоритми формування псевдовипадкових послідовностей з m-ічною основою
1. Вимоги, пропоновані до псевдовипадковим послідовностей.
2. Лінійна рекурентна послідовність з максимальным періодом.
3. Псевдовипадкова послідовність на базі многомодульных перетворень.
З класичної теорії стійкості й автентичності випливає, що передбачуваний рівень стійкості, що розраховується, і автентичності виходить у тому випадку, якщо загальносистемні параметри і ключ породжуються випадково, рівноймовірно і незалежно. Випадкові компоненти повинні формуватися на основі випадкових чи псевдовипадкових процесів. У ряді додатків необхідно застосовувати псевдовипадкові послідовності з необхідними властивостями.
Основні властивості:
1. Основа алфавіту - m.
2. Період повторення - L.
3. Відновлюваність.
4. Псевдовипадкові властивості.
5. Структурні властивості послідовностей.
На теперіщній час відомий ряд алгоритмів і засобів формування псевдовипадкових послідовностей. Основною їхньою особливістю є те, що вони будуються для 2-ічної основи (m=2). Відомий клас m – ічних послідовностей, володіє незадовільними структурними властивостями в змісті значної залежності появи символів послідовності. Для визначення закону формування таких псевдовипадкових послідовностей необхідно і досить одержати безпомилково 2l – символів, де l – база лінійного рекурентного регістра, тому дуже важливої і необхідний є задача розробки математичних алгоритмів і засобів побудови псевдовипадкової послідовності (ПСП) із заданими необхідними властивостями і підставою алфавіту m. До найбільш перспективному, на наш погляд, класу таких перетворень відноситься многомодульне перетворення.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.