Курс лекций по таможенной статистике, страница 60

7.6. Построение парного нелинейного уравнения связи. Прием

линеаризации переменных величин

      В реальности гораздо чаще встречаются связи нелинейного характера, которые могут быть отображены функциями разного вида:

- степенной ;

- логарифмической или ;

- показательной ;

- гиперболической 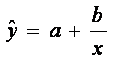  и другими.

      Для построения нелинейного парного уравнения регрессии проводят его линеаризацию, т.е. нелинейное уравнение приводят к виду, схожему с линейным. Например, для гиперболической функции необходимо заменить 1/x  на z. Тогда функция будет иметь вид: , т.е. вид, похожий на линейную форму уравнения. Для степенной функции линеаризация проводится следующим образом. Сначала выражение степенной функции логарифмируется, получаем: . Затем вводим обозначения, например, В результате получаем уравнение регрессии в виде: , похожем на линейную форму. К полученным выражениям функций применяем формулы для расчёта параметров a и b , соответствующие линейной форме, в которых вместо x будет стоять z (для гиперболического уравнения), либо Y, A, X (для степенного уравнения):

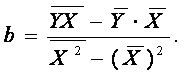
      Для нелинейных форм уравнений регрессии параметр b не является коэффициентом регрессии (кроме параболы второго порядка ).

7.7. Показатели тесноты парной нелинейной зависимости.

Их расчет и интерпретация

      Показателями тесноты парной нелинейной зависимости результата и фактора являются теоретическое корреляционное отношение или индекс корреляции , а также их квадраты, соответствующие коэффициенту детерминации. Теоретическое корреляционное отношение определяется по формуле: