Курс лекций по таможенной статистике, страница 59

7.5. Оценка качества уравнения регрессии

и существенности изучаемой связи

      Качество построенного уравнения регрессии оценивается с помощью средней ошибки аппроксимации. Такая оценка отвечает на вопрос о возможности использования полученного уравнения для дальнейшего анализа и прогнозирования.

      Средняя ошибка аппроксимации строится исходя из разности фактических значений результата и его теоретических значений, полученных по уравнению регрессии. Если фактические значения (у) и теоретические значения ( ) близки по величине, ошибка будет маленькой, если различия (у) и ( ) большие, ошибка будет большой. Средняя ошибка аппроксимации рассчитывается по формуле:

      Считается, что качество уравнения удовлетворительное и его можно использовать для анализа и прогнозирования, если  Если средняя

ошибка аппроксимации ещё меньше и не превышает 5%, то качество построенного уравнения считается очень хорошим.

      Оценка существенности уравнения связи проводится с использованием F-критерия Фишера. Выдвигается гипотеза о несущественности изучаемой связи признаков, т.е. о её случайном характере. Такая гипотеза называется нулевой и обозначается . Нулевую гипотезу необходимо проверить. Для этого рассчитывают фактическое значение критерия Фишера по формуле:

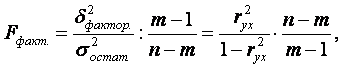
где  – факторная дисперсия (бо´льшая);

– остаточная дисперсия (меньшая);

n – число единиц совокупности;

m – число параметров уравнения регрессии;

m-1 – число степеней свободы факторной дисперсии;

n-m – число степеней свободы остаточной дисперсии;

– коэффициент детерминации.

      Фактическое значение критерия Фишера сравнивается с табличным значением, которое называется критическим. Критическое значение F- критерия определяется по таблице значений F-критерия Фишера при уровне значимости  (что соответствует вероятности P=95%) и соответствующих степенях свободы факторной и остаточной дисперсий. Критическое значение критерия Фишера – это максимальное значение, при котором принимается нулевая гипотеза . Затем фактическое значение критерия Фишера сравнивается с табличным (критическим). Если Fфакт. Меньше Fкрит. – нулевая гипотеза принимается и связь признаков признаётся несущественной (случайной). Если же Fфакт. больше Fкрит., то нулевая гипотеза отвергается, не принимается и связь признаков признаётся существенной, носящей закономерный характер.