2. Поясните принцип действия системы стабилизации промежуточной частоты.
3. Что называется дискриминационной характеристикой? Как влияет форма ДХ на показатели качества системы АПЧ?
4. Что называется регулировочной характеристикой? Как влияет ее форма на показатели качества системы АПЧ?
5. В чем заключаются особенности применения системы АПЧ качестве демодуляторов ЧМ-сигналов, следящего фильтра, формирователя ЧМ-сигналов?
6. Приведите математическое описание системы АПЧ.
7. Изобразите структурную схему системы АПЧ. формулируйте допущения, при которых она применима.
8. Приведите структурную схему линейной системы АПЧ сформулируйте условия ее применимости.
9. Как определяется частотная ошибка при типовых воздействиях (ступенчатом, линейном, квадратичном)?
10. Как определяется шумовая ошибка слежения за частотой? Какой смысл имеет шумовая полоса замкнутой системы? Как она связана с параметрами системы?
11. Каков физический смысл понятий полосы захвата и полосы удержания системы АПЧ? Как они связаны с параметрами системы?
ТЕМА 4: «СИСТЕМЫ ФАЗОВОЙ АВТОПОДСТРОЙКИ ЧАСТОТЫ»
Системы ФАПЧ также относятся к классу следящих систем и предназначены для слежения за фазой сигнала (точнее за частотой и фазой). В этом принципиальное отличие систем ФАПЧ от систем АПЧ, в которых информация о фазе сигнала теряется.
Благодаря этой особенности, системы ФАПЧ применяются гораздо шире, чем системы АПЧ. Они используются в качестве следящих фильтров доплеровских систем измерения скоростей, для стабилизации промежуточной частоты приёмников, синхронного детектирования сигналов, в качестве демодуляторов ЧМ- и ФМ-сигналов, в синтезаторах частот, в следящих измерителях координат (дальности, угла), для когерентного сложения сигналов в фазированных антенных решётках и прочее.
Принцип действия системы ФАПЧ рассмотрим на примере простейшей системы, описываемой функциональной схемой (рис. 4.1).
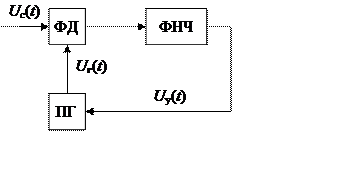
На входы фазового дискриминатора (ФД) поступает сигнал uc(t) (обычно промежуточной частоты) и опорное колебание uг(t), вырабатываемое подстраиваемым генератором. Если частоты сигнала и генератора совпадают (начальная частотная расстройка Df=fc–fг0=0), то в стационарном режиме напряжение на выходе ФД равно нулю, а фазовый сдвиг jст=jс – jг= –p/2.
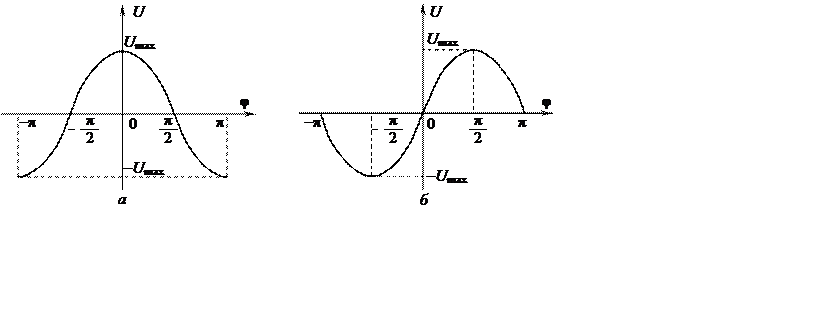
Объясняется это тем, что дискриминационная характеристика U(j) имеет вид функции косинуса (рис. 4.2, а).
Для того, чтобы придать дискриминационной характеристике вид нечётной (синусоидальной функции от j) (рис. 4.2, б), учтём фиксированный фазовый сдвиг на –p/2 (колебание генератора опережает сигнал на p/2 радиан) путём описания сигнала функцией синуса, а колебания генератора – функцией косинуса от j:
uc(t)=umcsinjc(t)=umcsin(wct+jc0),
uг(t)=umгcosjг(t)=umгcos(wгt+jг0).
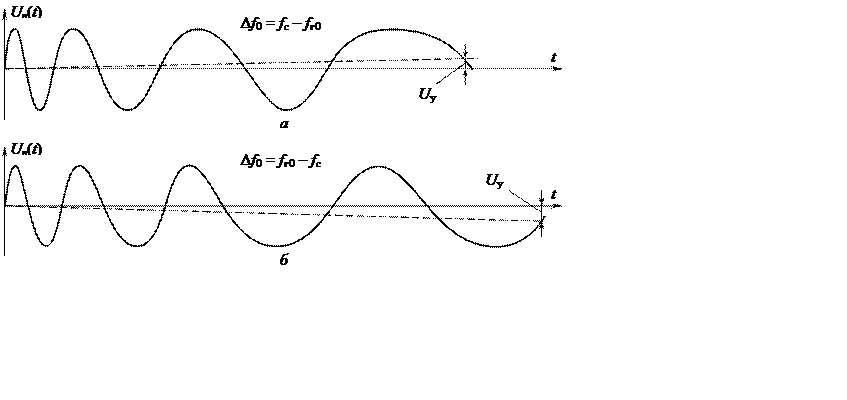
Рис.4.3
Обычно начальная расстройка Df0¹0 (вследствие нестабильности частот сигнала и подстраиваемого генератора, доплеровского сдвига частоты сигнала). В этом случае на выходе дискриминатора возникают биения с частотой Df. Если бы обратная связь была разомкнута, то на выходе ФД наблюдалось бы гармоническое колебание с частотой, равной частотной расстройке. Благодаря обратной связи управляющее напряжение Uу(t), воздействуя на подстраиваемый генератор (управляющий элемент – варикап), осуществляет частотную модуляцию колебания uг(t). В зависимости от знака управляющего напряжения частота биений то возрастает, то убывает (рис. 4.3). В результате длительности положительных и отрицательных полуволн напряжения биений оказываются разными, вследствие чего на выходе дискриминатора образуется постоянная составляющая напряжения, которая стремится уменьшить частоту биений до нуля. Фильтр нижних частот пропускает постоянное напряжение, обусловленное частотной модуляцией сигнала. Знак управляющего напряжения определяется знаком частотной расстройки: напряжение положительное при fc>fг0 (рис. 4.3, а) и отрицательное при fc<fг0 (рис. 4.3, б). В зависимости от знака Uу средняя частота генератора либо возрастает, либо убывает относительно начального значения fг0 (соответствует Uу=0), стремясь к значению, равному fc (рис. 4.4).
Если начальная расстройка не превышает значения Dfз, определяющего полосу захвата, то по истечении времени tз, называемого временем захвата, в системе устанавливается стационарный режим (режим слежения или удержания), при котором частотная расстройка Df=0 (fс=fг), а фазовый сдвиг сигнала относительно колебания генератора jст= –p/2+j, где j – фазовая ошибка (рис. 4.5). Если ФНЧ не содержит интегрирующих звеньев, то необходимое для компенсации частотной расстройки управляющее напряжение может быть выработано лишь в случае j¹0 (рис. 4.2, б). Причём, чем больше начальная расстройка, тем больше фазовая ошибка (максимальное значение имеет место при расстройке, равной полосе Dfз. При наличии хотя бы одного интегратора в составе ФНЧ, необходимое напряжение может быть сформировано, даже, если j=0, благодаря «памяти» фильтра (напряжение на выходе интегратора остаётся неизменным, хотя на входе его напряжение равно нулю). В этом случае фазовая ошибка обусловлена лишь воздействием шума, а также инерционностью системы (обычно j << p рад).
Если начальная расстройка Df0>Dfз, то управляющее напряжение становится недостаточным для её компенсации и установление стационарного режима невозможно. Этот режим (режим биений) характеризуется тем, что средняя частота генератора отличается от частоты сигнала, а разность фаз непрерывно нарастает (рис. 4.5, в).
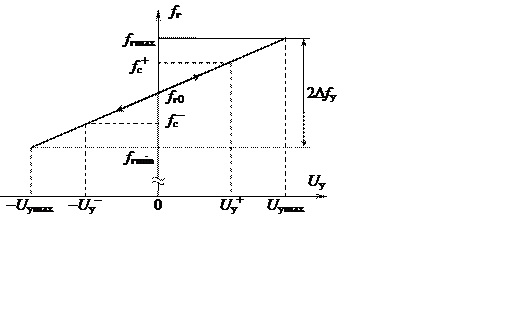
Полоса захвата системы ФАПЧ определяется диапазоном перестройки генератора, формой дискриминационной характеристики, а также структурой (видом передаточной функции) фильтра нижних частот. Определение её возможно лишь с использованием нелинейной теории и представляет весьма сложную задачу. Исключение составляет случай, не представляющий практического интереса, когда ФНЧ отсутствует. При этом имеет место равенство полос захвата и удержания. Последняя легко находится как 2Dfу=2Umax×kг, где Umax – пиковое значение дискриминационной характеристики (рис. 4.2), а kг – крутизна регулировочной характеристики (рис. 4.4).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.