Полагая усилитель безынерционным, для управляющего напряжения запишем
Uу(t)=kуUд(t), (6.6)
где kу – коэффициент усиления (на практике обычно используются корректирующие звенья, включённые в цепь отрицательной обратной связи усилителя; в этом случае вместо kу используется операторный коэффициент передачи Ку(p)).
Исполнительный двигатель описывается дифференциальным уравнением
,
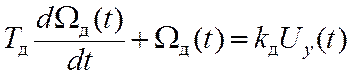где Wд(t) – управляемая переменная (скорость вращения ротора двигателя); kд – коэффициент передачи, имеющий размерность рад/сВ; Тд – постоянная времени, учитывающая инерционность как самого двигателя, так и следящей антенны.
Последнее уравнение представим в операторной форме:
,
(6.7)
где
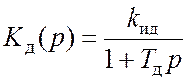– передаточная функция инерционного
звена, отображающего на структурной схеме исполнительный двигатель.
Редуктор осуществляет преобразование вращения ротора двигателя в угловое положение антенны. Математическим эквивалентом этого преобразования является операция
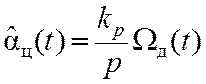, (6.8)
где kP – коэффициент передачи редуктора (интегрирующего звена).
Используя формулы (6.1)–(6.3), (6.6)–(6.8), запишем уравнение:
.
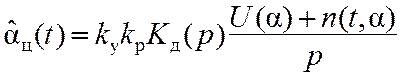(6.9)
Структурная схема ССН, построенная в соответствии с (6.9), представлена на рис. 6.3, а.
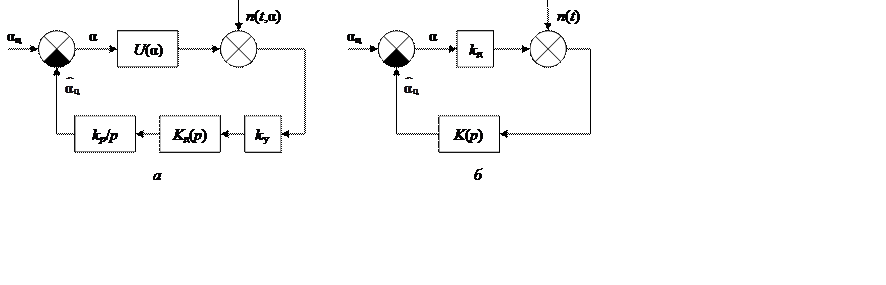
Рис. 6.3
Аппроксимируя дискриминационную характеристику
линейной зависимостью U(a)=kдa (kд – крутизна ДХ при a=0), что справедливо при малых ошибках a (режим
слежения), приходим к структурной схеме линейной системы (рис. 6.3, б). Передаточная
функц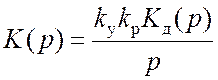ия 
. На основе линейной модели ССН можно
решать такие задачи как определение запаса устойчивости, качества переходного
процесса (быстродействия, перерегулирования), точности слежения.
Контрольные вопросы
1. Укажите области применения ССН.
2. Поясните принцип действия амплитудного пеленгатора с суммарно-разностной обработкой сигнала.
3. Какой вид имеет диаграмма направленности антенны автоматического радио пеленгатора?
4. Дайте математическое описание ССН.
5. Составьте структурную схему ССН.
6. Какой вид имеет структурная схема линейной ССН? При каких условиях она применима и какие задачи позволяет решать?
7. Как определяются динамические ошибки ССН при типовых воздействиях: скачкообразном, линейном, квадратичном?
8. Чем характеризуется точность ССН при воздействии помех? Какой смысл имеет шумовая полоса системы и как она определяется?
9. Как осуществляется поиск сигнала по направлению? Чем определяется полоса захвата ССН?
ЛЕКЦИЯ 6. ТЕМА 7: «ТИПОВЫЕ ЗВЕНЬЯ СИСТЕМ
РАДИОАВТОМАТИКИ»
Математические методы описания типовых звеньев.
Безынерционное (усилительное, пропорциональное) звено.
Инерционное звено (апериодическое звено первого порядка).
Интегрирующее звено.
Любое линейное звено может быть описано дифференциальным уравнением или передаточной функцией K(p),которая представляет оператор, показывающий, какие преобразования должны быть выполнены над входным сигналом x(t) для получения выходного сигнала y(t). Описание звена с помощью передаточной функции удобно и наглядно. Оно эквивалентно описанию с помощью дифференциального уравнения y(t)=K(p)x(t), где p=d/dt – оператор дифференцирования. К типовым относят такие звенья, которые описываются уравнением не выше второго порядка. Помимо операторного метода, базирующегося на понятии передаточной функции и использовании прямого и обратного преобразований Лапласа, при анализе систем радиоавтоматики широко используются частотный и временной методы.
Частотный метод основан на использовании преобразований Фурье и понятий комплексного коэффициента передачи K(jw) или его модуля K(w) – амплитудно-частотной характеристики (АЧХ) и аргумента j(w) – фазо-частотной характеристики (ФЧХ). Анализ систем существенно упрощается при использовании логарифмических частотных характеристик – амплитудных (ЛАХ) L = 20 lg K(w) и фазовых (ЛФХ). Объясняется это тем, что ЛАХ можно аппроксимировать отрезками прямых, имеющих определенный наклон. Кроме того, для построения ЛАХ используют простые выражения, так как в результате логарифмирования АЧХ произведения и частные от деления заменяют суммами и разностями. Основная область использования частотного метода – это анализ систем в установившемся режиме (определение запаса устойчивости, точности при воздействии помех).
Временной метод базируется на понятиях переходной h(t) и импульсной g(t) характеристик и связан с использованием интеграла Дюамеля (интеграла свертки). Наиболее часто этот метод используется для анализа систем в переходном режиме (определение быстродействия, перерегулирования и других показателей качества).
Уравнение динамики безынерционного звена – алгебраическое уравнение
y(t) = kx(t), (7.1)
где k – коэффициент усиления (или передачи).
Передаточная функция безынерционного звена
K(p) = Y(p)/X(p) = k.
Амплитудно-частотная и фазо-частотная характеристики определяются как K(w) = k и j(w) = 0 для всех w, а ЛАХ звена L(w) = 20lg k.
Переходная характеристика безынерционного звена аналогична по форме входному сигналу – ступенчатому воздействию: h(t) = kI(t), где I(t) – функция единичного скачка (равна единице при t ³ 0 и нулю при t < 0).
Импульсная характеристика звена также повторяет по форме входной сигнал: имеет вид дельта-функции d(t) (при t = 0 обращается в бесконечность, а при t > 0 – равна нулю).
Примерами конструктивного выполнения безынерционного звена являются потенциометр (аттенюатор), усилитель и др., если уравнения их динамики можно представить уравнением вида (7.1).
Уравнение динамики инерционного звена имеет вид
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.