Ошибка по ускорению в
системе второго порядка астатизма равна постоянной величине 
. Параметр K2,
характеризующий точность системы, называется добротностью по ускорению
(имеет размерность c –2).
Для исключения ошибки по ускорению можно использовать систему третьего порядка астатизма (с тремя интеграторами). Однако такие системы используются редко ввиду трудностей, связанных с обеспечением необходимого запаса устойчивости и качества переходного процесса.
Контрольные вопросы
1. Чему равна статическая ошибка для типовых САУ (статической, астатической первого и второго порядков)?
2. Как определяются динамические ошибки (по скорости, по ускорению) для статической и астатических систем?
ЛЕКЦИЯ 13. ТЕМА 12: «ТОЧНОСТЬ АВТОМАТИЧЕСКИХ СИСТЕМ
ПРИ ВОЗДЕЙСТВИИ ПОМЕХ»
Точность следящих систем при воздействии помех.
Дисперсия шумовой ошибки.
Шумовая полоса следящей системы.
Особенностью радиотехнических систем является то, что они работают в условиях воздействия помех, снижающих точность. Поскольку помехи (шумы, случайные отклонения параметров системы и прочее) - случайный процесс, то ошибка слежения в этих условиях также является случайной. Поэтому для характеристики точности следящих систем используются характеристики случайных процессов: среднее значение (математическое ожидание), дисперсия, средний квадрат.
При анализе точности следящих систем при воздействии помех удобно использовать структурные схемы, поясняющее образование ошибки слежения (рис. 12.1). На рис. 12.1, а ошибка образуется в результате сравнения задающего воздействия и управляемой величины, формируемой с помощью фильтра, описываемого передаточной функцией Kз(p) замкнутой системы. На входе фильтра действует смесь задающего воздействия x(t) и эквивалентного шума nэ(t)=n(t)/kд, имеющего размерность[x] (частоты, фазы и т. д., в зависимости от типа системы). Преобразование помехи n(t) в nэ(t) определяется правилом переноса узла суммирования через звено с коэффициентом передачи kд (см. лекцию 8).
Структурная схема (рис. 12.1, а) может быть преобразована к виду (рис. 12.1, б), где ветвь с передаточной функцией 1–Kз(p) определяет динамическую ошибку eд(t), обусловленнуюотличием передаточной функции замкнутой системы от идеальной Kз(p)=1, а ветвь с передаточной функцией Kз(p)определяет ошибку – en(t) из-за воздействия помехи.
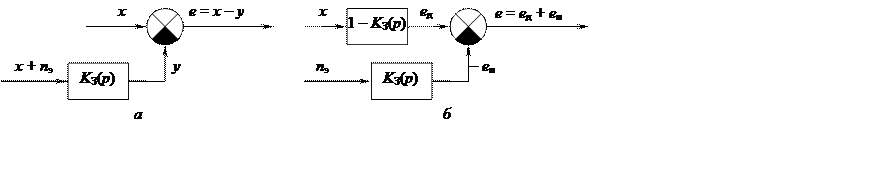
Рис. 12.1
Ошибка en(t) случайна. Если помеха представляет стационарный случайный процесс с нулевым средним значением и спектральной плотностью Sn(w), то ошибка en(t) - также стационарный случайный процесс с нулевым средним значением и дисперсией s2.
В зависимости от характера воздействия x(t) (детерминированное или случайное) точность следящих систем в условиях действия помех оценивается либо средним квадратом
(12.1)
либо дисперсией
(12.2)
результирующей ошибки e(t).
Значение динамической ошибки eд определяет в (12.1) математическое ожидание (среднее значение) ошибки слежения при детерминированном воздействии. Если задающее воздействие представляет стационарный случайный процесс с нулевым средним значением и спектральной плотностью Sx(w), то динамическая ошибка eд(t) - также стационарный случайный процесс с нулевым средним значением и дисперсией s2ед (дисперсия ошибки равна сумме дисперсией обеих её составляющих, так как процессы n(t) и x(t) независимы ).
Дисперсия шумовой ошибки в соответствии с рис. 12.1, б определяется как
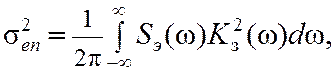(12.3)
где Sэ(w)=Sn(w)/k2д - энергетический спектр эквивалентного шума, а Sn(w) – энергетический спектр помехи n(t) на выходе дискриминатора.
Для практических приложений правомерно полагать n(t) белым шумом с равномерным спектром Sn(f)=N0 Вт/Гц в полосе частот от 0 до ¥ (рис. 12.2, а) (или с двухсторонним спектром Sn(w)=N0/2). При этом эквивалентный шум также является белым со спектральной плотностью мощности Sэ(f)=Nэ=N0/k2д, имеющей размерность [х]2/Гц ([х] – размерность задающего воздействия).
Используя для описания помехи модель белого шума, представим выражение (12.3) для дисперсии шумовой ошибки в виде
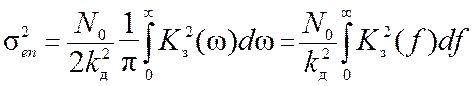. (12.4)
Интеграл в (12.4) определяет так называемую шумовую полосу замкнутой системы
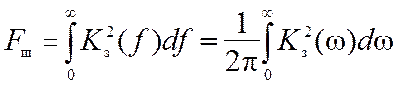. (12.5)
Физический смысл параметра Fш состоит в том, что квадрат АЧХ реальной замкнутой системы аппроксимируется идеальной прямоугольной характеристикой (рис. 12.2, б) при условии равенства дисперсий ошибок (дисперсия определяется площадью заштрихованной фигуры).
Формула (12.5) справедлива для астатических систем, значение АЧХ которых Kз(0)=1 (статические системы для слежения за параметрами сигналов не используются из-за больших динамических ошибок).
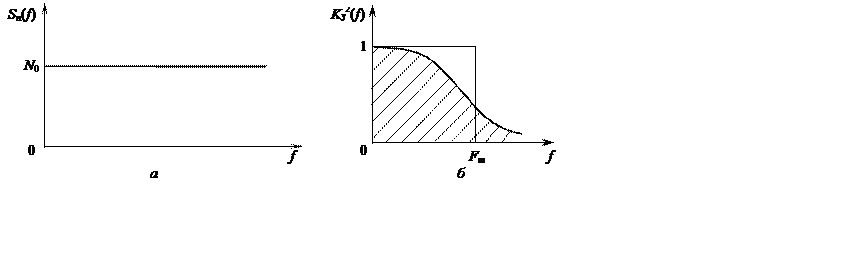
Рис. 12.2
С учетом (12.5) формулу (12.4) перепишем в виде
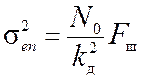. (12.6)
При заданной спектральной плотности N0 определение дисперсии шумовой ошибки сводится к вычислению шумовой полосы системы. Для типовых систем радиоавтоматики определенный интеграл в (12.5) сводится к табличному интегралу
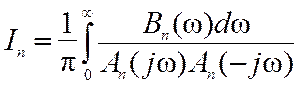, (12.7)
где полиномы An(jw) и Bn(w) определяются как
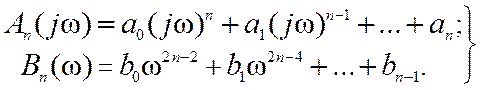(12.8)
Для систем, описываемых дифференциальными уравнениями порядка n£3, значения табличного интеграла равны
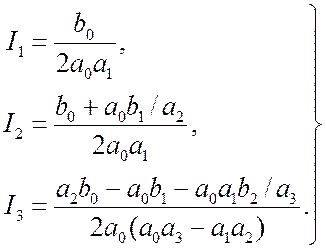(12.9)
Дисперсия динамической ошибки при случайном воздействии в соответствии с рис. 12.1, б определяется выражением
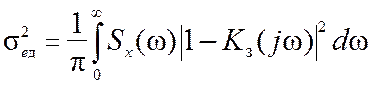. (12.10)
При известном энергетическом спектре Sx(w) вычисление s2ед сводится к вычислению определённого интеграла вида (12.7). В тех случаях, когда интеграл (12.10) не удается свести к табличному, используют численные методы интегрирования или графический метод. В последнем случае необходимо иметь графики спектральной плотности Sx(w) и квадрата АЧХ KЗ(w)=|1–KЗ(w)|. Тогда, перемножив их при одних и тех же значениях частоты, можно построить график спектральной плотности Sед(w)динамической ошибки (рис. 12.3, а). Далее можно определить площадь, ограниченную осью частот и кривой Sед(w), и после деления на p получить значение s2ед. Аналогично можно определить дисперсию шумовой ошибки (см. рис. 12.3, а).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.