Метод моделирования на ЭВМ (иначе имитационное моделирование) является универсальным методом анализа нелинейных систем как при детерминированном воздействии, так и при случайном воздействии. Благодаря большим вычислительным возможностям современных компьютеров он позволяет определять статистические характеристики (средние значения ошибок слежения, среднеквадратические отклонения ошибок и пр.) при различных моделях сигналов и помех. При числе испытаний 103 и более метод статистического моделированияпозволяет с высокой достоверностью определить важнейшие характеристики АС на этапе ее проектирования (без проведения дорогостоящих и затратных по времени экспериментальных исследований).
Радиотехнические следящие системы, как правило, работают в условиях, когда начальное рассогласование (ошибка e) превышает «раскрыв» дискриминационной характеристики. Способность системы «захватывать» сигнал и осуществлять слежение при максимально допустимой расстройке характеризуют полосой захвата, определение которой для каждого типа систем имеет свои особенности, но в целом она определяется раскрывом ДХ. Устранение начальной расстройки (уменьшение ее до значений, определяемых полосой захвата) достигается применением специальной процедуры, называемой поиском сигнала. Другая особенность радиотехнических следящих систем связана с тем, что они всегда работают в условиях действия различного рода помех, затрудняющих осуществление захвата и приводящих, зачастую, к явлению, называемому срывом слежения. Это имеет место, когда расстройка по какой-либо причине выходит за пределы раскрыва ДХ (система «размыкается»). Анализ работы следящих систем в режимах, связанных с захватом сигнала или срывом слежения, проводится с использованием нелинейной модели (обобщенная структурная схема на рис.15.1).
Рассмотрим задачу анализа нелинейной АС на примере наиболее известной и широко применяемой в радиотехнике системы АПЧ.
15.1. Анализ нелинейной системы АПЧ
Анализ проведем при следующих допущениях:
а) частотный дискриминатор – безынерционное нелинейное звено со статической характеристикой U(Δf);
б) помеха отсутствует ( на вход ЧД поступает только полезный сигнал);
в) частотная расстройка Δfc=const (модель скачкообразного постоянного задающего воздействия);
г) собственный шум подстраиваемого генератора отсутствует (нестабильность частоты ПГ δfг→0);
д) в качестве ФНЧ используется инерционное звено с передаточной функцией Kф(p)=1/(1+Тp) (статическая система АПЧ).
Сформулированным предпосылкам соответствует структурная схема на рис. 15.1.
Рис.15.1
Дифференциальное уравнение для рассматриваемой системы имеет вид
(15.1)
Подставив в (15.1) выражение для Kф(p), может записать
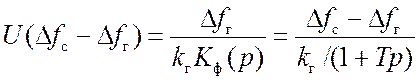
или 
В установившемся режиме (при t→∞ или p→0) имеем
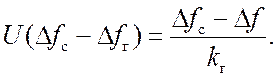(15.2)
Нелинейное алгебраическое уравнение (15.2) может быть решено с использованием графо-аналитического метода. На рис.15.2 представлены: дискриминационная характеристика (кривая 1) и прямая линия 2 (правая часть уравнения), проведенная с наклоном – 1/kг через точку Δfc на оси абсцисс.
 |
|||||
 |
|||||
 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
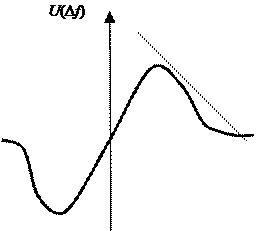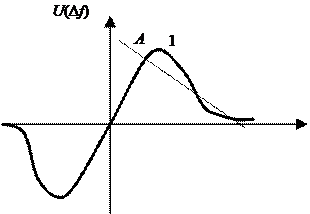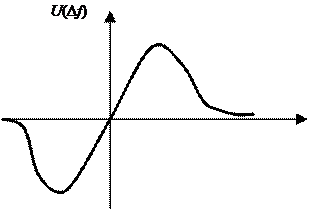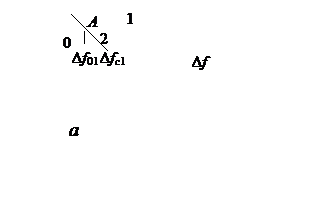
Рис.15.2
Как видно из рисунка, при малом значении Δfc (рис. 15.2,а) имеется всего лишь одна точка А устойчивого равновесия, соответствующая решению уравнения 15.2: Δf=Δf0, Δf0 – остаточная частотная расстройка. При Δfc1→0 значение Δf0 совпадает со значением статической ошибки Δfcт= Δfc1/(1+K0), найденным с использованием линейной теории (см. лекцию 6).
При значении частотной расстройки Δfc2 (рис.15.2,б) имеется три точки: А, В и С, соответствующие решению уравнения (15.2). Причем точками устойчивого равновесия являются лишь две точки: А и С, а точка В соответствует состоянию, в котором система не может находиться в установившемся режиме. Покажем это используя алгебраический критерий устойчивости – критерий Гурвица. Полагая возмущение малым, что позволяет аппроксимировать ДХ в окрестности каждой из точек А, В и С линейными отрезками с крутизной kA, kВ и kС соответственно, для передаточной функции замкнутой (линеаризованной) системы можем записать
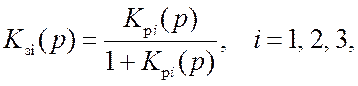
где
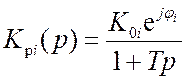(15.3)
–
передаточная функция разомкнутой системы, соответствующая точкам А, В и
С (
), 
и
– модуль и аргумент комплексного
коэффициента передачи разомкнутой системы (k1= kА ,k2 =kВ ,k3 =kС).
Используя (15.3), запишем систему уравнений (характеристические уравнения)
где 
(15.4)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.