(10.4)
Для обеспечения малой колебательности и большого быстродействия системы необходимо выбрать её структуру и параметры так, чтобы АЧХ имела малый пик и широкую полосу пропускания (максимальное значение wср ограничивается воздействием на систему помех). По техническим требованиям величина М должна выбираться в пределах 1,2–1,5, а wср определяется по заданному времени tп.
Рис. 10.3
Построение характеристики Kз(w) производят по АФХ разомкнутой системы, учитывая что
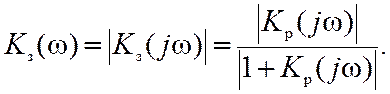(10.5)
В соответствии с (10.5) значение Kз(wi) на какой-либо частоте wi определяется отношением длин (модулей) двух векторов Kp(jwi) и 1+Kp(jwi), определяемых точкой АФХ разомкнутой системы для частоты wi (рис. 10.5). Находя это отношение для других точек АФХ (при других частотах), можно построить характеристику Kз(wi).
Рис. 10.4
Из рисунка (10.5) видно, что при малых частотах (w®0) значение Kз(w)@1, а при больших частотах (w®0) величина Kз(w)®0. Чем ближе АФХ Kр(jw) расположена к критической точке (–1, j0), тем больше значение Kз(w) по сравнению с единицей (в случае, когда АФХ проходит через критическую точку, знаменатель в (10.5) обращается в нуль, а сама АЧХ Kз(w) - в бесконечность).
В идеальной системе Kз(w)=1 для всех частот, а соответствующая этому АФХ имеет вид прямой, проходящей параллельно мнимой оси через точку –0,5 на оси абсцисс (рис. 10.5, б).
Если АФХ проходит при некоторых частотах левее (кривая 1), то АЧХ замкнутой системы имеет пик. В этом случае переходный процесс будет колебательным с перерегулированием. Точка пересечения АФХ с линией 2 определяет частоту среза wср.
Если АФХ не заходит в область слева от линии 2 (кривая 3), то АЧХ замкнутой системы является убывающей функцией, а переходный процесс - монотонным.
Рис. 10.5
В результате исследования АС с различным видом ЛАХ установлено, что колебательность переходного процесса будет наименьшей, если частота среза wср разомкнутой системы находится на участке ЛАХ с наклоном – 20 дБ/дек. При этом время переходного процесса определяется неравенством
. (10.6)
В отличие от (10.4) частота среза wср в (10.6) определена для разомкнутой, а не для замкнутой системы.
Чем шире участок ЛАХ с наклоном – 20 дБ/дек, пересекающий ось абсцисс, тем ближе переходная характеристика к экспоненте и тем меньше время tп (тем ближе оно к значению p/wср). Этот участок следует выбирать при расчете параметров системы в соответствии с заданными показателями качества.
Практическое применение ЛАХ разомкнутой системы для косвенной оценки качества переходного процесса основано на использовании универсальных переходных характеристик и типовых ЛАХ.
Для АС, составленных из типовых звеньев, произведена классификация ЛАХ и вычислены универсальные характеристики, построенные для нормированного времени (рис. 10.6).
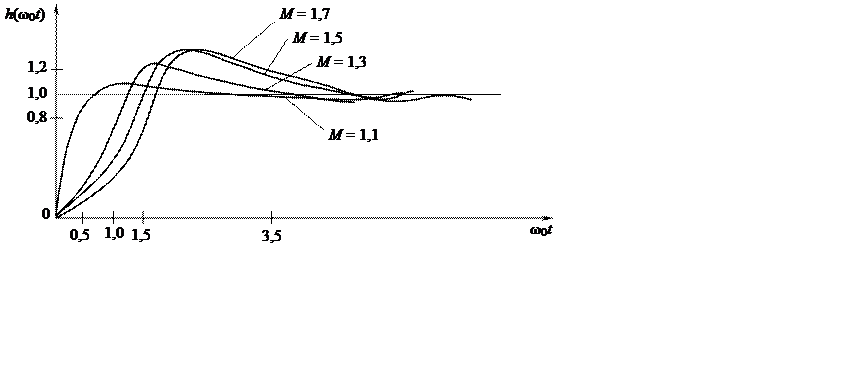
Рис. 10.6
Выбор нужной универсальной характеристики h(w0t) производится на основе типовых ЛАХ и параметров системы. Затем, разделив масштаб по оси абсцисс на w0, получают искомую переходную характеристику.
Типовые ЛАХ для наиболее распространенных на практике систем с астатизмом первого и второго порядка (не путать с порядком уравнения, описывающего систему) представлены на рис. 10.7 (астатическим системам первого порядка соответствуют ЛАХ на рис. 10.7, а, б, а системам второго порядка – ЛАХ на рис. 10.7, в, г).
ЛАХ, изображенные на рис. 10.7, отличаются от рассмотренных ранее тем, что по оси абсцисс откладывается нормированная «частота» w/w0, а точки сопряжения асимптот определяются значениями относительных «постоянных времени» ti=w0Ti.
Базовая частота w0 в зависимости от порядка астатизма определяется следующими выражениями:
- для систем первого
порядка,
- для систем второго
порядка (К – общее усиление разомкнутой системы).
Значение показателя колебательности определяется по известным w0 и wср из табл. 10.1.
Таблица 10.1
|
wср/w0 |
3, 35 |
2, 08 |
1, 73 |
1, 56 |
|
М |
1, 1 |
1, 3 |
1, 5 |
1, 7 |
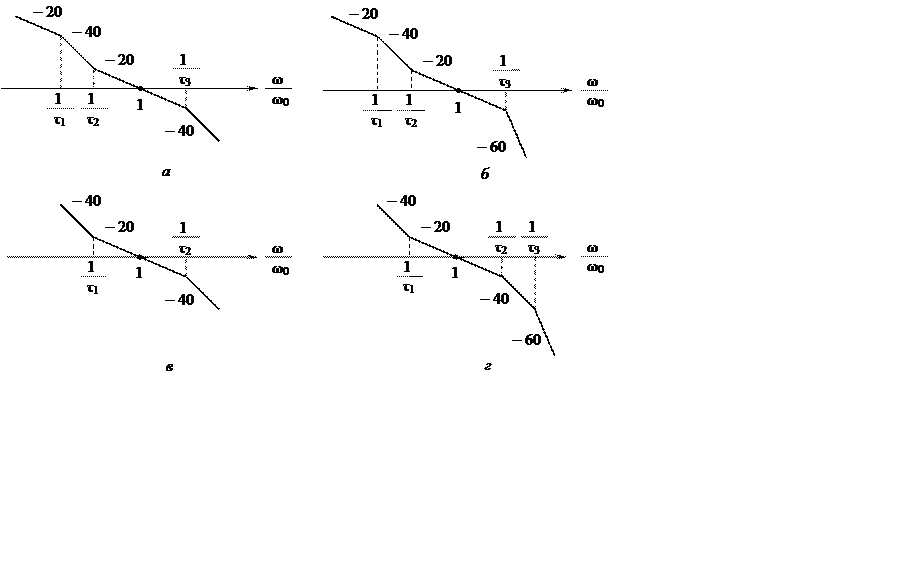
Рис. 10.7
Возможность использования универсальных переходных характеристик независимо от порядка астатизма системы указывает на то, что вид участка ЛАХ при низких частотах (– 20 дБ/дек и – 40 дБ/дек соответственно для систем первого и второго порядков) мало влияет на характер переходного процесса. Форма этого участка ЛАХ определяет ошибку системы в установившемся режиме. Аналогично вид участка ЛАХ на высоких частотах (– 40 дБ/дек или – 60 дБ/дек) также мало влияет на форму переходной характеристики (он определяет лишь передний фронт характеристики).
Таким образом, качество переходного процесса определяется, главным образом, участком ЛАХ с наклоном – 20 дБ/дек, который должен иметь протяженность не менее декады и располагаться по возможности симметрично относительно частоты среза. Это гарантирует хорошие показатели качества переходного процесса (малую колебательность, небольшое перерегулирование и малое время переходного процесса).
Контрольные вопросы
1. Назовите основные показатели качества САУ.
2. В чем различие прямых и косвенных методов оценки качества переходного процесса?
3. Дайте характеристику монотонного, апериодического и колебательного переходных процессов.
4. Назовите основные показатели качества переходного процесса. Как они определяются по переходной характеристике?
5. Дайте характеристику метода цифрового моделирования непрерывных систем.
6. Как определяются показатели качества переходного процесса по АЧХ замкнутой системы?
7. Как оценивается качество переходного процесса по ЛАХ разомкнутой системы? Каким требованиям должна удовлетворять ЛАХ?
ЛЕКЦИЯ 12. ТЕМА 11: «ТОЧНОСТЬ АВТОМАТИЧЕСКИХ СИСТЕМ
ПРИ ТИПОВЫХ ВОЗДЕЙСТВИЯХ»
Статические и динамические ошибки типовых САУ.
Статическая ошибка для типовых САУ (статической, астатической первого и второго порядков).
Астатические системы автоматического управления.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.