Радиоавтоматика: основы теории и принципы построения автоматических систем, страница 33

Квазинепрерывный метод анализа цифровых систем РА

Рассмотрим сущность указанного метода анализа применительно к цифровой системе ФАПЧ (рис.18.2), широко используемой в практических приложениях.

Вых.демод.

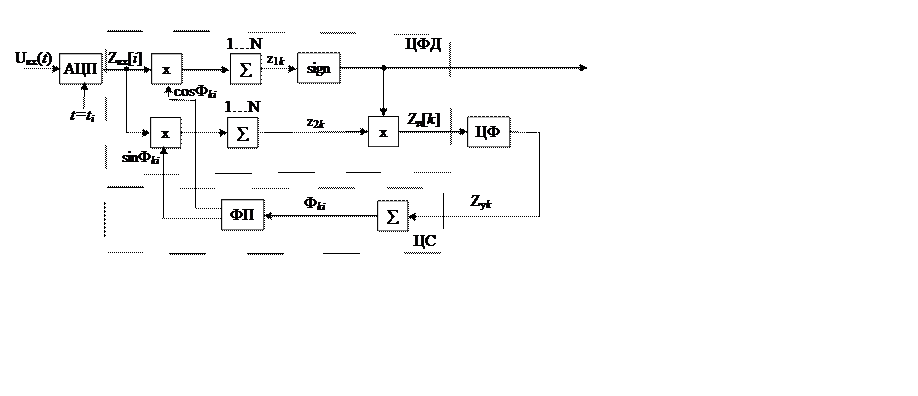
Рис.18.2

Как видно из рисунка, в данном примере АЦП расположен до контура регулирования. На вход системы поступает сигнал U_вх(t), являющийся аддитивной смесью полезного сигнала U_c(t)=D(t)U_c(t)cos[ω₀t–φ(t)]и шума U_ш(t). Здесь U_c(t) – огибающая сигнала (закон амплитудной модуляции), D(t)€{+1,      –1} – цифровое сообщение, передаваемое методом фазовой манипуляции (ФМ). С помощью АЦП, осуществляющего дискретизацию в моменты t=t_i=iΔt(i=0,1,…; Δt–интервал дискретизации) и квантование, входной сигнал преобразуется в цифровой сигнал оператор квантования.

В цифровом фазовом дискриминаторе (ЦФД) входной сигнал Z_вх[i] перемножается с двумя квадратурными сигналами частоты ω_k:  cosω_kt_i и sinω_kt_i, формируемыми функциональным преобразователем (ФП). Значение ω_k=ω₀[k] – это оценка несущей частоты ω₀ на k–м шаге фильтрации (k=0,1,2…). Каждый шаг фильтрации включает в себя интегрирование квадратурных видеочастотных сигналов на интервале Т и формирование сигнала ошибки:

гдеz_1k=z₁[k]и z_2k=z₂[k]– результаты интегрирования в квадратурных каналах ЦФД (выход синфазного канала является выходом демодулятора цифрового сообщения). Величины z_1k  и  z_2k формируются с помощью цифровых интеграторов (накапливающих сумматоров ), опрашиваемых в моменты t=kt, k=1,2,..; T=NΔt–интервал дискретизации сигнала ошибки, n–целое. Необходимость интегрирования (накопления) в каналах ЦФД обусловлена тем, что отношение сигнал/шум в линейной части (до нелинейных элементов «sign» (знаковая функция) и перемножителя (на выходе дискриминатора)части ()тношение сигнал/шум в линейно  демодулятора цифрового сообщенияирование сигнала ошибки.

ены в виде  о) должно быть достаточно большим, чтобы исключить подавление слабого сигнала шумом (см. лекцию 7). Это в частности необходимо при слежении за фазой шумоподобных сигналов, когда отношение сигнал/шум на входе дискриминатора g_вх<<1.

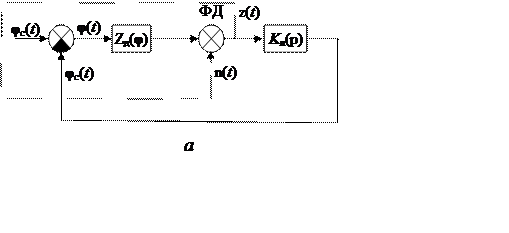
Полагая дискриминатор безынерционным, что справедливо при F_ш<< F_д, представим структурную схему цифровой системы ФАПЧ в виде нелинейной квазинепрерывной модели системы, изображенной на рис.18.3,а. На этом рисунке  K_л(p)– эквивалентная передаточная функция линейной части, n(t)–белый шум со спектральной плотностью N_д, z_э(t)– процесс на выходе эквивалентного непрерывного дискриминатора: z_э(t)=z_д(k) при                                      (k–1)T≤t≤kT(кусочно-постоянный сигнал).

При переходе к непрерывной модели суммирование в линейной части заменяется интегрированием:

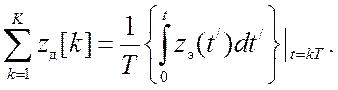
Модель на рис.18.3,а можно исследовать методами теории непрерывных систем. С другой стороны, параметры модели (через дискриминационную и флуктуационную характеристики) существенно зависят от частоты дискретизации и числа уровней квантования. Это позволяет отразить многие существенные особенности поведения цифровой системы.

Дальнейшее упрощение связано с «линеаризацией» нелинейной модели рис.18.3,а, основанной на аппроксимации дискриминационной характеристики: Z_д(φ)≈k_дφ (см. лекцию 6). Модель на рис.18.3,б отображает линейную астатическую следящую систему (астатизм обусловлен наличием интегрирующего звена в передаточной функции K_л(p)). Линейную модель можно исследовать методами теории линейных систем автоматического регулирования. Вместе с тем эта модель (при выполнении условий ее применимости) правильно отражает основные существенно нелинейные свойства цифровой системы (зависимость шумовой полосы от отношения сигнал/шум, влияние шума на быстродействие системы и др.). Нелинейный характер цифровой системы отображается при расчете параметров квазилинейной модели (k_д и N_д).

Передаточная функция квазилинейной замкнутой системы

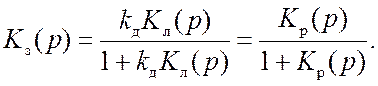                                                                     (18.1)

Важнейшим параметром линейной системы является шумовая полоса F_ш (определение F_ш дано в лекции 9).

z(t)

б

n(t)

φc(t)

φ(t)

φc(t)

Kл(p)

kд

Рис.18.3

   Наибольшее применение на практике находят астатические цифровые системы ФАПЧ с порядком астатизма i≤2. На рис.18.4 представлена квазилинейная  модель следящей системы 2-го порядка астатизма (пунктиром обведена структура астатического фильтра с передаточной функцией K_ф(p)).

Используя (18.1) с учетом того, что передаточная функция астатического фильтра (содержащего интегрирующее звено) K_ф(p)=k₁(1+T₁p)/p(T₁=1/k₁–постоянная времени форсирующего звена),находим передающую функцию замкнутой системы (рис.18.4)

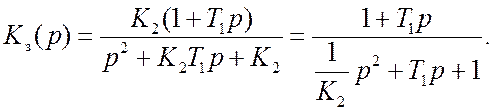                                                     (18.2)

гдеK₂ =k_дk₁k₂–добротность системы по скорости.

Как следует из (18.2) замкнутая система эквивалентна последовательному соединению форсирующего звена с передаточной функцией (1+T₁p) и колебательного звена с параметрами T=1/, и коэффициентом передачи, равным единице (см.лекцию 7). Исследуемая система имеет два регулируемых параметра: k=k_дk₂ и k₁. Если эти параметры изменять таким образом, чтобы оставалось постоянным их отношение , то это будет соответствовать изменению временных и частотных характеристик системы типа «сжатие-растяжение» по оси абсцисс. При этом остаются неизменными такие важные показатели, как запас устойчивости, качество переходного процесса и др.