Радиоавтоматика: основы теории и принципы построения автоматических систем, страница 25

Определение динамических ошибок (по скорости, по ускорению) для статической и астатических систем.

Точность АС характеризуется величиной ошибки в установившемся режиме и зависит от характера воздействия, а также структуры и параметров системы.

Реальные воздействия в радиотехнических следящих системах описывается сложными (случайными) функциями времени. Однако при анализе точности управления часто используют простые детерминированные воздействия: постоянное ступенчатое, линейное, квадратичное и другие. Это позволяет упростить анализ и в то же время сохранить в модели задающего воздействия наиболее существенные признаки (начальное значение, скорость изменения, ускорение). Большинство систем радиоавтоматики описываются передаточными функциями вида

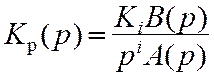,                                                 (11.1)

где K_i - общее усиление разомкнутой системы, i – число интегрирующих звеньев, определяющее порядок астатизма системы;

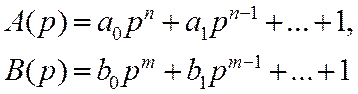
– полиномы, порядок которых определяется числом типовых звеньев (n и m соответственно инерционных и форсирующих), а коэффициенты полиномов – постоянными времени типовых звеньев.

11.1. Статические ошибки

Ошибка системы при постоянном (ступенчатом) воздействии x(t)=x₀=const при t³0 называется статическойe_ст.

Для установившейся ошибки, учитывая, что изображение X(p)=x₀/p, запишем:

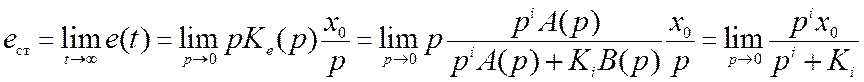.  (11.2)

Для статической системы (не содержащей интегрирующих звеньев) статическая ошибка равна

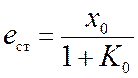.                                                                      (11.3)

Таким образом, в статических системах установившееся значение управляемой переменной не равно заданному: меньше на величину ошибки, значение которой обратно пропорционально усилению К₀ по постоянному току (обычно К₀>>1).

Для астатических систем (i ³ 1) ошибка при постоянном воздействии

,

так как числитель в (11.2) равен нулю, а знаменатель равен К_i.

Отсутствие статической ошибки обусловило название таких систем – астатические.

11.2. Динамические ошибки

Ошибка, характеризующая точность замкнутой системы при меняющемся воздействии, называется динамической e_д(t).

Любое детерминированное воздействие (при условии существования его производных d^(k)/dt^(k), k=1, 2, …) можно представить в виде ряда

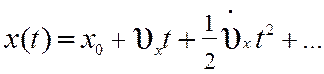,                                  (11.4)

где x₀ - начальное значение,  - скорость изменения, - ускорение и т. д.

Для вычисления динамических ошибок при типовых воздействиях (линейном и квадратическом) представим выражение для ошибки в операторной форме:

                                   (11.5)

Используя разложение передаточной функции K_e(p) в ряд Маклорена по степеням переменной р, перепишем (11.5) в виде

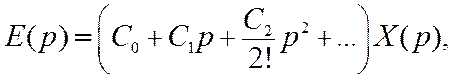                           (11.6)

где C₀, C₁, C₂, … - коэффициенты ошибок, определяемые как

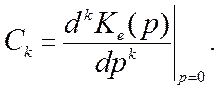                                        (11.7)

Установившееся значение ошибки при произвольном воздействии x(t) на основании (11.6) определяется временным рядом

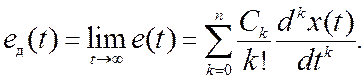                                       (11.8)

Чем меньше коэффициенты ошибок, тем выше точность системы при произвольном детерминированном воздействии. При вычислении коэффициентов C_k обычно ограничиваются только первыми тремя (для систем с астатизмом не выше второго порядка).

Коэффициент C₀ в соответствии с (11.7) равен

.

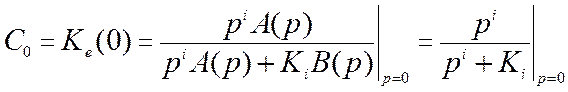Для статических систем (i=0) C₀=1/(1+K₀), а для астатических систем C₀=0.

Определим динамические ошибки типовых систем при линейном воздействии (изменение с постоянной скоростью) x(t)=n_xt.

В соответствии с формулой (11.8) динамическая ошибка (ошибка по скорости) определяется как

.

Для статической системы она равна

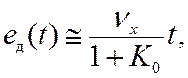
так как вклад составляющей C₁n_x значительно меньше, чем C₀ x(t), которая растет линейно со временем. Таким образом, скоростная ошибка в статических системах накапливается со временем со скоростью n_x/(1+K₀), что делает неприемлемым использование таких систем при меняющемся воздействии. Для астатических систем C₀=0 и скоростная ошибка

.

Нахождение коэффициента ошибки C₁ с использованием формулы (11.7) затруднительно. Более простой способ его вычисления основан на сравнении точного выражения для передаточной функции K_e(p) и аппроксимирующего ее ряда:

                (11.9)

Уравнение (11.9) можно представить в виде

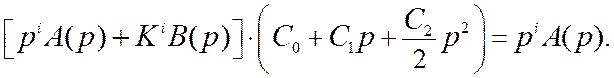              (11.10)

Полагая i= 1 (астатическая система первого порядка) и приравнивая коэффициенты при переменной p в левой и правой частях уравнения, находим

или C₁=1/K₁, так как C₀=0.

Таким образом, скоростная ошибка системы первого порядка астатизма e_д=n_x/K₁ определяется усилением разомкнутой системы K₁ и не зависит от времени. Параметр K₁, имеющий размерность c ^–1, называется добротностью системы по скорости (чем выше добротность, тем точнее система).

Для астатической системы второго порядка скоростная ошибка равна нулю, так как оба коэффициента C₀=C₁=0. Равенство C₁=0 вытекает из уравнения (11.10), так как в правой части уравнения не содержится слагаемого, в которое входит переменная p (есть только с p² и выше).

Оценим динамические ошибки типовых систем при квадратичном воздействии (изменение с постоянным ускорением).

В соответствии с (11.8) для динамической ошибки (ошибки по ускорению) запишем

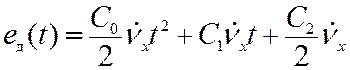.                                        (11.11)

Для статической системы ошибка по ускорению равна

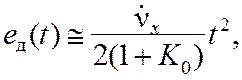                                    (11.12)

так как составляющие ошибки с коэффициентами C₁ и C₂ вносят пренебрежимо малый вклад в результирующую ошибку. Накопление ошибки по квадратичному закону исключает применение статических систем при наличии ускорения.

Для системы первого порядка астатизма ошибка по ускорению равна

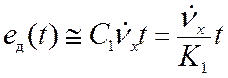                                      (11.13)

(вкладом составляющей  можно пренебречь). Накопление ошибки со временем (со скоростью ) не позволяет применять такие системы при наличии ускорения. Для астатической системы второго порядка ошибка по ускорению равна

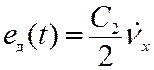.                                      (11.14)

Определение коэффициента ошибки C₂ с использованием уравнения (11.7) сводится к приравниванию коэффициентов при p² в обеих частях уравнения:

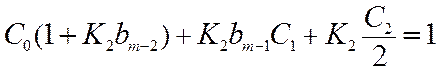.                           (11.15)

Откуда C₂/2=1/K₂, так как C₀=C₁=0.