Методы анализа качества переходного процесса можно разделить на две группы. К первой относятся прямые методы оценки качества по переходной характеристике, ко второй - косвенные методы. Прямые методы требуют решения дифференциальных уравнений (или экспериментальных исследований). Косвенные методы позволяют, не решая уравнений, определять некоторые показатели качества.
Графически требования, предъявляемые к качеству процесса управления, можно определить некоторой областью (рис. 10.1), за пределы которой управляемая переменная не может выходить. Основными параметрами заданной области качества процесса управления являются: время переходного процесса tп, заданное значение x0, ошибка d и максимальное превышение emax управляемой переменной. Область заданного качества расположена либо относительно линии заданного значения x0 (рис. 10.1, а), либо относительно оси абсцисс, если рассматривается переходный процесс для ошибки (рис. 10.1, б).
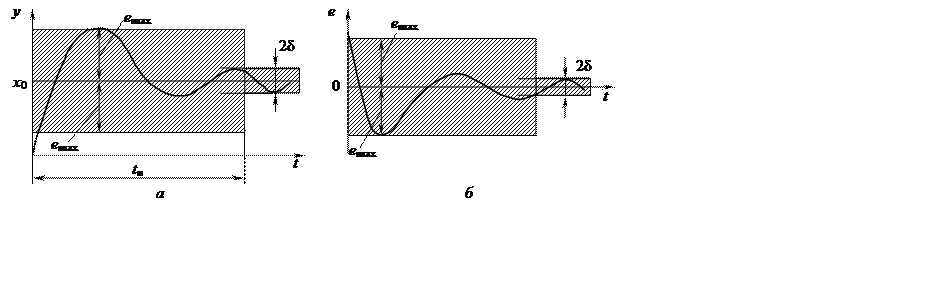
Рис. 10.1
В зависимости от характера затухания при скачкообразном воздействии переходный процесс может быть монотонным, апериодическим или колебательным (рис. 10.2). Процесс является монотонным, если ошибка при t®¥ только уменьшается (кривая 1); процесс считается апериодическим, если имеет место не более одного перерегулирования (кривая 2); процесс называется колебательным, если управляемая переменная в течение переходного процесса несколько раз отклоняется в обе стороны от установившегося значения (кривая 3).
Если управляемая переменная принимает значение, большее x0, вводится понятие о максимальном отклонении emax. При больших emax могут возникнуть чрезмерные перенапряжения в элементах системы. Поэтому значения emax ограничивают в техническом задании на проектирование. Максимальное отклонение, выраженное в процентах, называют перерегулированием e=(emax/x0)×100%. Обычно для АС принимают допустимым e £ 30%.
Быстродействие системы определяется временем переходного процесса tп, под которым понимают время, по истечении которого ошибка управления не превосходит заданной величины d (рис. 10.2). Обычно принимают d £ 5% от значения x0.
Для оценки быстроты затухания колебательного переходного процесса, наряду со временем tп, используют понятие о степени колебательности m, которая характеризуется числом колебаний в системе за время переходного процесса. Значение m не должно быть большим, так как колебания в системе нежелательны (могут привести к износу механических элементов и др.).
Рис. 10.2
Для оценки качества переходного процесса в непрерывной системе можно использовать метод моделирования, в соответствии с которым непрерывная система заменяется дискретной, а дифференциальное уравнение, описывающее систему, – разностным уравнением. Последнее представляет собой программу рекуррентного вычисления переходного процесса. Применение ЭВМ позволяет легко решить это уравнение, т. е. рассчитать переходный процесс.
Дискретная передаточная функция цифровой модели получается из передаточной функции непрерывной системы путем замены оператора интегрирования 1/р некоторым оператором, соответствующим тому или иному численному методу интегрирования.
Наиболее часто используется замена
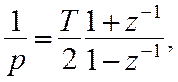(10.1)
где T - интервал дискретизации, z=e pT - переменная Z – преобразования (z – 1=e – pT - оператор задержки на T).
Аппроксимация непрерывного интегратора дискретным (10.1) соответствует интегрированию по методу трапеций. При T®0 переходные процессы в непрерывной системе и её цифровой модели будут близки друг к другу. На практике достаточно обеспечить условие Т<<p/wср, где wср - частота среза АЧХ непрерывной системы (иногда вместо wср берётся значение полосы на уровне 0,7).
Полученную в результате замены (1.69) передаточную функцию цифровой модели системы необходимо представить в виде дробно-рациональной функции по степеням z – 1:
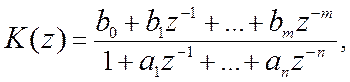(10.2)
что позволяет определить коэффициенты аi(i=1, 2, …, n) и bi(i=1, 2, …, m) разностного уравнения. Передаточной функции (10.2) соответствует разностное уравнение для управляемой переменной
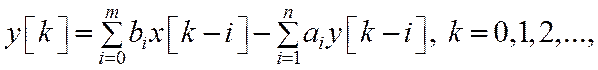(10.3)
где y[k] - текущее значение управляемой переменной, x[k–i] и y[k–i] - предыдущие значения процессов на (k–i)-м шаге (при отрицательном аргументе равны нулю).
Рекуррентное уравнение (10.3) определяет переходный процесс при дискретном времени, кратном интервалу дискретизации Т. Качественные показатели переходного процесса (перерегулирование, быстродействие и др.) определяют по графику зависимости y[k] или e[k] (коэффициенты разностного уравнения для ошибки находят по передаточной функции Ke(p)).
Один из косвенных методов оценки качества переходного процесса основан на использовании АЧХ замкнутой системы. Если система неустойчива, то амплитуда колебаний на выходе системы достигает бесконечно большой величины (в реальных системах она ограничена из-за нелинейности характеристик). В этом случае АЧХ системы имеет разрыв (рис. 10.3, а).
В зависимости от соотношения параметров АЧХ устойчивой замкнутой системы либо имеет пик, либо является убывающей функцией частоты (кривые 1–4, рис. 10.3, а).
Уменьшение пика АЧХ соответствует уменьшению амплитуды и числа колебаний, совершаемых системой в переходном режиме. На рис. 10.3, б показаны переходные характеристики при различных соотношениях параметров системы в соответствии с характеристиками KЗ(w). Анализ кривых, имеющих одинаковые номера, свидетельствует о том, что с уменьшением максимума АЧХ процесс затухает быстрее. При убывающей характеристике KЗ(w)(кривая 4) переходный процесс является монотонным (без перерегулирования).
Следовательно, пик АЧХ может служить косвенной оценкой величины перерегулирования и колебательности процесса. При этом отношение максимума характеристики KЗ(w) к значению при w=0 называется показателем колебательности М (для астатических систем K(0)=1 и М равен максимуму АЧХ). Частота, при которой АЧХ имеет максимум, называется собственной частотой w0 (рис. 10.4). Если характеристика имеет пик, то точка пересечения кривой с линией KЗ(0)=1 определяет частоту wср замкнутой системы. Эта частота косвенно характеризует быстродействие системы. Чем больше частота wср, тем выше быстродействие. При этом время переходного процесса
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.