Радиоавтоматика: основы теории и принципы построения автоматических систем, страница 34

Для определения оптимального значения параметра η обратимся к характеристикам колебательного звена (знаменатель, выражения 18.2). Важнейшими его параметрами являются собственная частота w₀=и коэффициент затухания  Для удовлетворительного качества переходного процесса коэффициент затухания должен выбираться из условия 0,5≤η≤1, что соответствует значениям параметра η: 1≤ η ≤4. При η>4 переходной процесс монотонный (без перерегулирования), а при η<4–колебательный (с перерегулированием ε<30%).

   Система (рис.18.4) устойчива при любых значениях параметров kи k₁, что позволяет оценивать только запас устойчивости по фазе . Минимально допустимому значению соответствует значение η=0,6.

На рис.18.5 представлены графики АЧХ K₃(f) замкнутой системы, построенные при значении η=0,5;4 и 10³(кривые 1,2 и 3 соответственно) по формуле

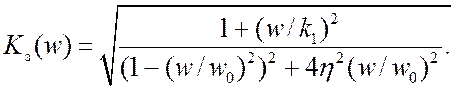
Для того, чтобы при различных kи k₁ (но постоянном η) можно было пользоваться одним графиком, по оси абсцисс на рис.18.5 откладывается безразмерная «частота» f/F_ш. Шумовая полоса в соответствии с (10.6) равна

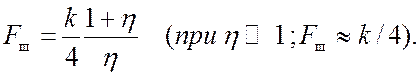
Как видно из рисунка, при любом η значение АЧХ при f=0 равно единице (признак астатической системы). Это означает отсутствие статической ошибки в установившемся режиме. При η<0,5 такое значение K_3макс>1,5, что свидетельствует о чрезмерно большом перерегулировании (ε>30%).

На рис.18.6 представлены графики переходного процесса для фазовой ошибки при скачкообразном постоянном воздействии   Для удобства используются нормированные величины: по оси ординат–нормированная фазовая ошибка , а по оси абсцисс–безразмерное «время» F_шt.

Как следует из анализа представленных характеристик, зависимость качества переходного процесса от параметра η выражена весьма заметно. Для значений η от 1 до 4 перерегулирование не превышает допустимого: ε<30%. Время переходного процесса (по критерию 5% от начального значения) определяется выражением.

Динамическая ошибка в установившемся режиме определяется как

φ_д=φ_с/K_2,

где φ_с=d² φ_с(t)/dt²–ускорение, с которым изменяется задающее воздействие φ_с(t) (пологам φ_с=const).

Можно показать, что оптимальное значение параметра η, при котором достигается минимальная динамическая ошибка (при фиксированном значении F_ш, а значит и дисперсии шумовой ошибки–см.лекцию 8) равно η_опт=1. В этом случае φ_д=φ_с/4F_ш².

Таким образом, значение η=1 удовлетворяет требованием заданного качества переходного процесса и точности слежения в установившемся режиме.

 

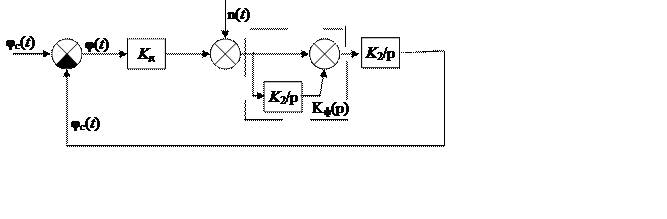Рис.18.4

tFш

φ(t)/φc

-0,5

-0,25

0,25

0,5

0

1

0,75

4

1

2

3

1

2

3

                                   

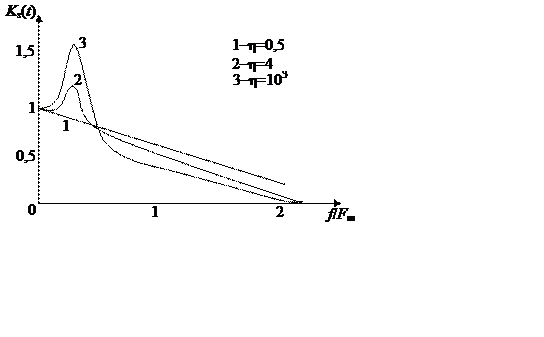
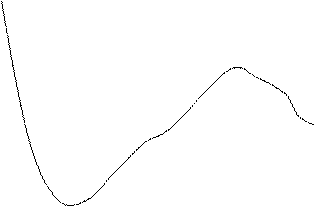
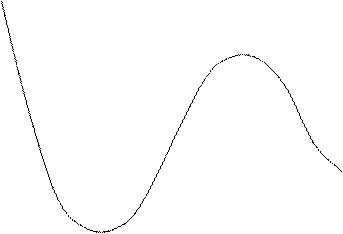
 Рис.18.5                                                                           Рис.18.6                                 

Напомним, что используемая линейная модель следящей системы применима для режима работы, при котором мала вероятность выхода значения фазовой ошибки φ за пределы линейного участка дискриминационной характеристики. Это условие может быть выполнено только при большом отношении сигнал/шум в эквивалентной полосе F_ш системы. При малом отношении сигнал/шум на входе дискриминатора (это имеет место, например, в системах слежения за фазой периодического шумоподобного сигнала) требуются очень малые значения шумовой полосы (менее 0,1Гц). Достижение таких значений F_ш в аналоговых системах практически не возможно, в то время как цифровые системы ФАПЧ позволят достичь значений F_ш порядка 0,01Гц с использованием современной цифровой элементной базы.

Контрольные вопросы

1. Сформулируйте основные преимущества цифровых САУ перед аналоговыми системами.

2. Изобразите обобщенную функциональную схему цифровой следящей системы и укажите назначения ее элементов.

3. Дайте краткую характеристику квазинепрерывного метода анализа цифровых систем.

4. Каковы условия применимости квазинепрерывного метода анализа цифровых систем?

5. Каким образом нелинейный характер цифровой системы отображается в линеаризованной модели?

Библиографический список

1. Бондаренко, В.Н. Теория управления и радиоавтоматика: Учебное пособие. Красноярск: КГТУ, 1999.

2. Бондаренко, В.Н. Основы автоматики: Учебное пособие. Красноярск: ИПЦ КГТУ, 2005.

3. Первачёв, С.В. Радиоавтоматика. – М.: Радио и связь, 1982.

4. Бесекерский, В.А. Теория систем  автоматического управления / В.А.Бесекерский, Е.П.Попов.СПб.: Профессия, 2003.

5. Коновалов, Г.Ф. Радиоавтоматика. – М.: Высш. шк., 1990.

6. Ерофеев, А.А. Теория автоматического управления. СПб.: Политехника, 1998.

7. Бесекерский, В.А. Радиоавтоматика /Под ред. В. А. Бесекерского. – М.: Высш. Шк.,1985.

8. Яшугин, Е. А. Теория линейных непрерывных систем автоматического управления в вопросах и ответах / Е. А. Яшугин. – Минск.: Вышейшая школа, 1986.

9. Шахгильдян, В.В., Ляховкин А.А. Системы фазовой автоподстройки частоты. М.: Связь, 1972.