Радиоавтоматика: основы теории и принципы построения автоматических систем, страница 19

Дискриминационная характеристика имеет ограниченный раскрыв 2De, определяемый допустимым значением напряжения U_доп (рис. 8.3, б). Обычно полагают U_доп =0,lU_max (U_max – пиковое значение ДХ). Если ошибка выходит за пределы раскрыва ДХ, то происходит срыв слежения (система размыкается). Для первоначального ввода в режим слежения, а также повторного – при срыве слежения (из-за воздействия помех, потери сигнала и т. д.) – требуется принудительное уменьшение ошибки до значения, определяемого раскрывом ДХ. Эта операция носит название поиска сигнала (по параметру х). Наряду с дискриминационной важной характеристикой дискриминатора является его флуктуационная характеристика (ФХ), под которой понимается зависимость дисперсии помехи n(t,e) от ошибки.

Рис. 8.3

Обычно полоса предшествующего дискриминатору приёмного тракта много больше полосы тракта, включенного за дискриминатором. Это позволяет полагать n(t,e) белым шумом со спектральной плотностью N₀(e) Вт/Гц. Поскольку мощность белого шума равна бесконечности, то под ФХ понимают зависимость от ошибки не дисперсии, а спектральной плотности помехи на выходе дискриминатора (рис. 8.4).

Рис 8.4

Форма N₀(e) зависит от усиления предшествующего тракта, способа нормировки сигнала, отношения сигнал/шум, типа дискриминатора и его параметров.

В соответствии с обобщенной структурной схемой (рис. 8.2) можно записать дифференциальное уравнение системы (в операторной форме):

y(t)=K(p)[U(e)+n(t,e)].                                      (8.2)

Это нелинейное стохастическое (вероятностное) уравнение. Нелинейность его обусловлена тем, что характеристики дискриминатора U(e) и N₀(e) нелинейны, а вероятностный характер – случайными функциями n(t,e) и x(t), так как воздействие полагается случайным. Анализ системы, описываемой уравнением (1.42), – чрезвычайно трудная задача. Поэтому стремятся упростить математическое описание системы. Упрощение достигается заменой нелинейного звена с характеристикой U(e) линейным звеном с коэффициентом передачи, равным крутизне ДХ (рис. 8.3, б)

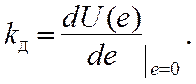
Линеаризация дискриминационной характеристики справедлива, если ошибка e® 0, что обычно имеет место на практике (высокая точность слежения). При этом флуктуационная характеристика может полагаться не зависящей от ошибки, т. е. N₀(е) =N₀ = соnst.

С учётом аппроксимации характеристик дискриминатора уравнение (8.2) принимает вид

у(t)=k_Д К(р)е(t) +K(p)n(t).                                        (8.3)

Структурная схема линейной системы, описываемой этим уравнением, представлена на рис. 8.5.

С использованием этой схемы могут быть решены такие задачи, как определение запаса устойчивости, быстродействия, точности слежения и другие. При этом тип системы не имеет значения, т. е. линейная модель, представленная на рис. 8.5, справедлива для описания любой следящей системы при условии, что ошибка слежения мала. Структурные схемы реальных следящих систем отличаются от линейной модели, однако, используя определённые правила преобразования структурных схем их всегда можно свести к данной схеме.

Рис. 8.5

8.2. Правила преобразования структурных схем

        Последовательное соединение звеньев. Это такое соединение, когда выходная переменная каждого предыдущего звена является входным воздействием для последующего звена (и только для него одного) (рис. 8.6).

Передаточная функция последовательно соединённых звеньев равна произведению их передаточных функций:

.

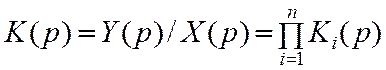Рис. 8.6

       Параллельное соединение звеньев. Это такое соединение, когда на вход всех звеньев подается один и тот же сигнал, а выходная переменная равна сумме выходных переменных звеньев (рис. 8.7).

При параллельном соединении п звеньев эквивалентная передаточная функция

.

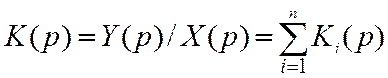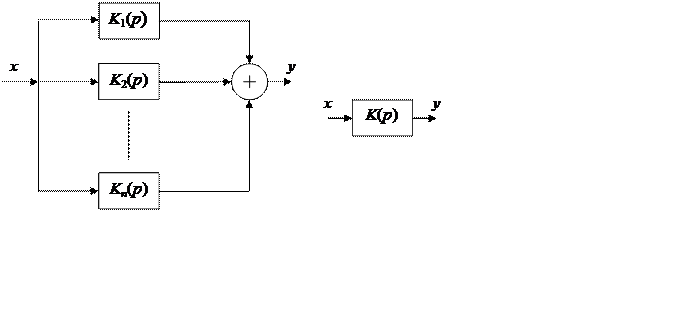
Рис. 8.7

        Встречно-параллельное соединение звеньев. При таком соединении звеньев на вход звена подается не только входная переменная, но и выходная переменная по цепи отрицательной обратной связи (рис. 8.8).

Рис. 8.8

Передаточная функция эквивалентного звена равна

.

Перенос узла суммирования через звено (рис. 8.9, а). В зависимости от направления переноса сумматора преобразованная структурная схема принимает следующий вид: рис. 8.9, б соответствует переносу сумматора «против хода сигнала», а рис. 8.9, в –  «по ходу сигнала». 

                 

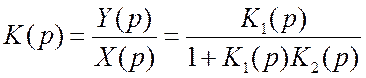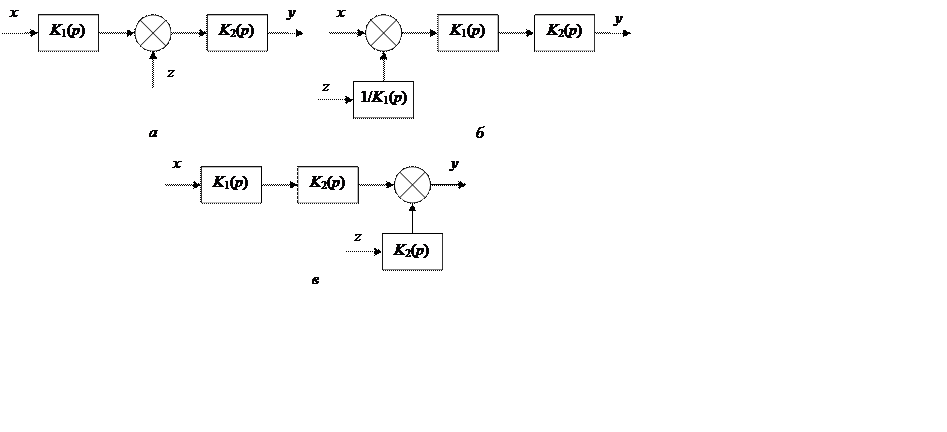
Рис. 8.9

 

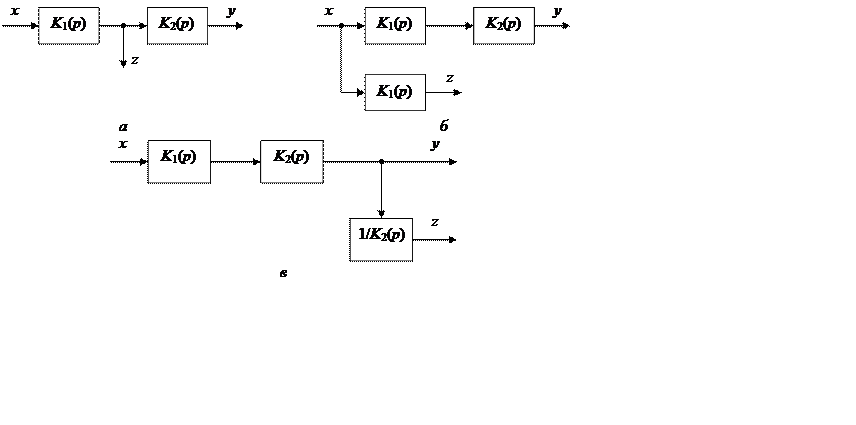
Рис. 8.10

        Перенос точки разветвления через звено (рис. 8.10, а). Данное преобразование иллюстрируется рисунком (переносу «против хода сигнала» соответствует схема на рис. 8.10, б, а «по ходу сигнала» –     рис. 8.10, в).

8.3. Передаточные функции замкнутой системы

При анализе замкнутых систем часто полагают, что помеха (возмущение) отсутствует (например, при анализе устойчивости или точности при детерминированном воздействии). Это позволяет представить обобщённую структурную схему, изображённую на рис. 8.5, в виде схемы (рис. 8.11).

Рис. 8.11

Используя изложенные правила преобразования (последовательное и встречно-параллельное соединения звеньев), для передаточной функции замкнутой системы можем записать:

  

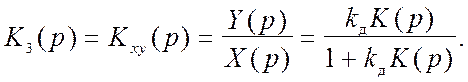
(8.4)

В ряде задач (например, при анализе точности при типовых воздействиях) необходимо знать передаточную функцию «от воздействия к ошибке»,     т. е.

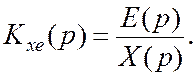
Рассматривая последовательно соединённые звенья (рис. 8.11) как цепь обратной связи (ошибка e в данном случае является выходной переменной) и используя правило преобразования при встречно-параллельном соединении звеньев находим

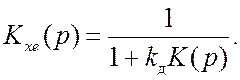                                              (8.5)

Сравнивая выражения (8.4) и (8.5), замечаем, что между указанными передаточными функциями существует однозначное соответствие:

.                                               (8.6)

При исследовании точности следящих систем при воздействии помех требуется знание передаточной функции «от помехи к ошибке»:

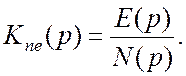
Для её нахождения преобразуем обобщённую схему (рис. 8.5) в схему (рис.8.12).

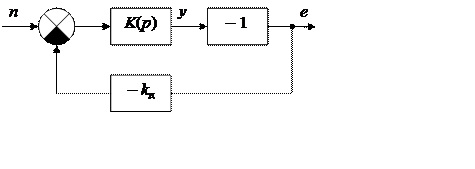
Рис. 8.12