Радиоавтоматика: основы теории и принципы построения автоматических систем, страница 17

Графики частотных характеристик (ЛАХ и ЛФХ) форсирующего звена отличаются от представленных на рис. 7.2 соответствующих характеристик инерционного звена лишь тем, что наклон асимптоты L²(w), а также знак фазы положительны.

Рис. 7.7

Переходная характеристика форсирующего звена изображена на   рис. 7.7. Она содержит две составляющих: первая имеет вид дельта-функции, что соответствует дифференциальной составляющей правой части уравнения (7.16), а вторая – ступенчатой функции, соответствующей пропорциональной компоненте уравнения.

Форсирующее звено относится к корректирующим звеньям, вводимым в систему с целью обеспечения заданных характеристик (запаса устойчивости, точности и т. д.). Поскольку идеальных дифференцирующих звеньев создать невозможно, то практическая реализация форсирующих звеньев осуществляется с использованием других типовых звеньев. Например, параллельное соединение безынерционного (пропорционального) и интегрирующего звеньев (рис. 7.8, а) эквивалентно последовательному соединению форсирующего звена и интегратора (рис. 7.8, б) с общей передаточной функцией

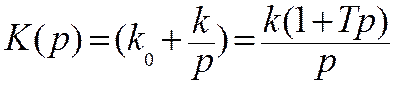,                        (7.22)

где 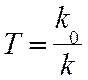 – постоянная времени, а k – общий коэффициент передачи.

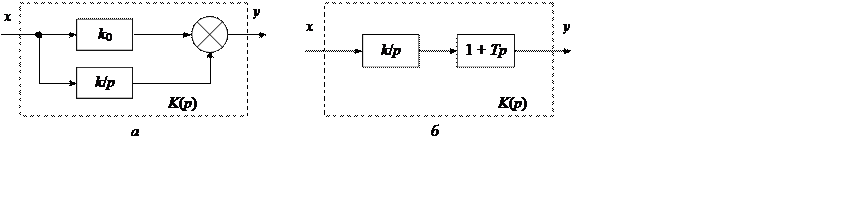
Рис. 7.8

Нетрудно убедиться, что в обоих случаях передаточная функция определяется выражением (7.22).

Другой способ реализации форсирующего звена основан на использовании так называемого пропорционально-интегрирующего фильтра (рис. 7.9).

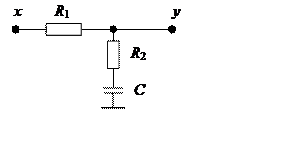
Рис. 7.9

Передаточная функция такого фильтра имеет вид

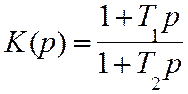,                                           (7.23)

где постоянные времени Т₁=R₂C и Т₂=(R₁+R₂)C.

Фильтр нижних частот с передаточной функцией (7.23) можно представить как последовательное соединение двух типовых звеньев: форсирующего и инерционного с общим коэффициентом передачи k=1.

7.5. Колебательное звено

Уравнение динамики колебательного звена имеет вид

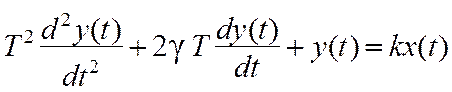,                          (7.24)

где  Т – постоянная времени, g – коэффициент затухания (демпфирования), k – коэффициент передачи.

Передаточная функция, соответствующая уравнению (7.24), равна

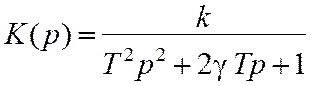.                                    (7.25)

Частотные характеристики можно определить, используя выражение (7.25). При этом АЧХ и ФЧХ  колебательного звена определяются выражениями:

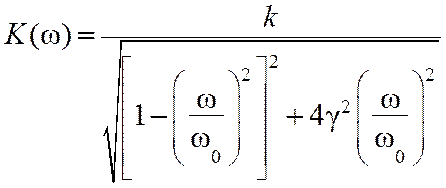,                           (7.26)

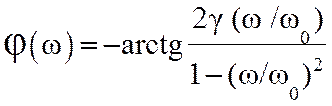             ,                                             (7.27)

где w₀=1/Т - собственная частота.

Графики частотных характеристик, построенные в соответствии с формулами (7.26), (7.27) для различных значений g, представлены на        рис. 7.10 (g₁>1, g₂=1, g₃=0,5, g₄<0,5).При значениях коэффициента затухания g<0,5 амплитудная частотная характеристика имеет ярко выраженный максимум, который смещается влево по оси частот по мере увеличения затухания (типичными для радиоавтоматики являются значения g=0,5-0,7).

Резонансная частота определяется как w_р=w₀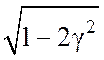. Значение АЧХ на этой частоте K_max=K(w_р)=k/(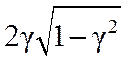), а на частоте w₀ равно K(w₀)=k/2g. При  g ³ 0,7 АЧХ становится монотонно убывающей (отсутствует резонансный выброс).

При значениях коэффициента затухания g ³ 1 звено становится апериодическим (второго порядка). Оно эквивалентно последовательному соединению двух инерционных звеньев (апериодических первого порядка).

ЛАХ колебательного звена определяется на основании выражения (7.26):

L(w)=20lgK(w)=20lgk– 20lg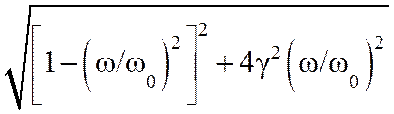.    (7.28)

Аналогично тому, как это было выполнено для инерционного звена, ЛАХ колебательного звена можно заменить приближенной ЛАХ в виде двух асимптот. Первая асимптота характеризует ЛАХ при малых частотах, когда вместо (7.28) можно приближенно принять

L¢(w)20lgk.                                     (7.29)

Вторая асимптота характеризует ЛАХ при больших частотах, когда вместо (7.28) можно полагать

L²(w)20lgk – 40lg(w/w₀).                               (7.30)

Эта асимптота зависит от частоты: изменение частоты на одну декаду влечет уменьшение усиления на 40 дБ. Построенные по формулам (7.29), (7.30)   ЛАХ отличаются от соответствующих характеристик инерционного звена (рис. 7.2) лишь тем, что наклон их при частотах w>w_c=w₀ составляет   – 40 дБ/дек. Максимальная погрешность аппроксимации точной ЛАХ соответствует частоте сопряжения w_с. Считается, что такая аппроксимация вполне приемлема, если коэффициент затухания g = 0,5-0,7.

Рис. 7.10

Переходная характеристика колебательного звена определяется выражением

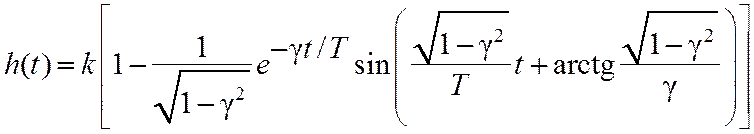 при g<1.  (7.31)

Графическое изображение переходной характеристики при k=1 приведено на рис. 7.11. Время переходного процесса, определяемое как время, по истечении которого отклонение выходной величины от установившегося значения не превышает 5%, определяется как t_п. Период собственных колебаний Т₀ равен .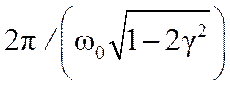

 

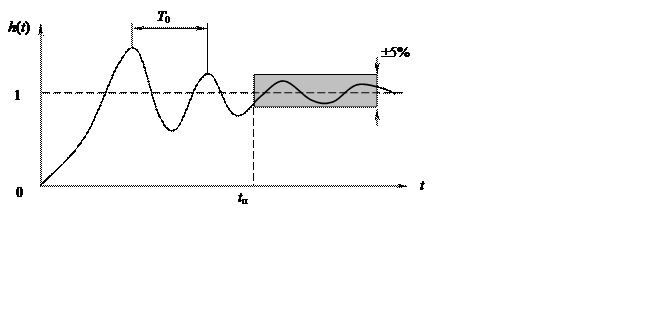
Рис. 7.11

Примерами выполнения колебательных звеньев являются: колебательный контур, центробежный маятник, электродвигатель постоянного тока и    т. д., если уравнения их динамики можно представить в виде (7.24).

Контрольные вопросы

1. Дайте краткую характеристику операторному, частотному и временному методам анализа линейных элементов и систем.

2. Что называется передаточной функцией элемента (системы)? Как получить эту функцию по известному дифференциальному уравнению?

3. Какие динамические звенья называют типовыми? Назовите основные типовые звенья САУ. Укажите примеры элементов САУ, которые могут быть описаны типовыми звеньями (для каждого типового звена).

4. Какой вид имеют уравнения динамики типовых звеньев?

5. Приведите выражения для передаточных функций типовых звеньев?

6. Какой вид имеют частотные характеристики (АЧХ, ФЧХ) типовых звеньев? Какими выражениями они описываются?

7. Как строятся ЛАХ и ЛФХ типовых звеньев? Что дает использование логарифмических частотных характеристик для исследования САУ?

8. Что называется амплитудно-фазовой характеристикой элемента (системы)? Как строятся АФХ типовых звеньев систем радиоавтоматики?