Развитие цифровой элементной базы (внедрение в практику цифровой номенклатуры МПК, многоразрядных АЦП, ПЛИС и других БИС) позволяет реализовать алгоритмы, близкие к оптимальным, создавать малогабаритные, экономически выгодные цифровые системы РА.
Математическое описание дискретных систем РА
Для анализа и синтеза дискретных (в том числе и цифровых) систем РА используется математический аппарат Z-преобразования, краткое изложение которого содержится в данной лекции (подробное знакомство с математическим аппаратом дискретных систем будет вам предложена в рамках дисциплины «Цифровая обработка сигналов»).
Дискретное преобразование Лапласа записывается в виде
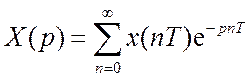 (16.1)
(16.1)
Функцию
![]() называют дискретной или решетчатой.
называют дискретной или решетчатой.
Введем
переменную ![]() . Тогда выражение (16.1) принимает
вид
. Тогда выражение (16.1) принимает
вид
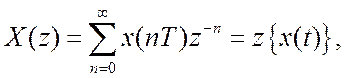 (16.2)
(16.2)
где
![]() – оператор задержки на T,
Т – интервал дискретизации.
– оператор задержки на T,
Т – интервал дискретизации.
Функцию
Х(z) называют Z-преобразованием
непрерывной функции х(t) (![]() Z-преобразования).
Z-преобразования).
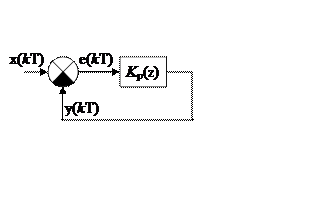
Передаточные функции дискретной замкнутой системы (рис.16.1,а) определяются аналогично передаточным функциям непрерывных систем. Так передаточная функция «от воздействия х к управляемой переменной у»
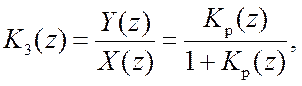 (16.3)
(16.3)
а передаточная функция «от воздействия х к ошибке e»
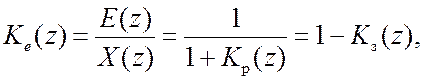 (16.4)
(16.4)
гдеX(z), Y(z) и E(z) – Z-преобразования соответствующих переменных, Kp(z)–передаточная функция разомкнутой системы.

|
|
Рис.16.1
Как и для непрерывных систем, может быть составлена обобщенная структурная схема(рис.16.1,б) радиотехнической следящей дискретной системы (линейная модель), где x(kT), y(kT), e(kT) и n(kT) – дискретные функции, описывающие задающее воздействие, управляемую переменную, ошибку и помеху на выходе дискриминатора в моменты t=kT, k=0,1…
С использованием передаточных функций (16.3), (16.4), а также структурной схемы рис.16.1, можно записать разностное уравнение системы (аналог дифференциального уравнения для непрерывной системы)
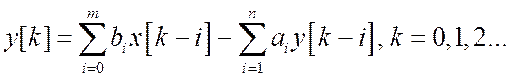 (16.5)
(16.5)
гдеy[k]=y(kT) – значение управляемой на текущем k-м шаге, x[k–i]=y[k–i]–предыдущие значения дискретных функций на (k–i)-м шаге (при отрицательном аргументе равны нулю).
Коэффициенты ai (i=0,1,2…,n) и bi(i=1,2,…,m) определяются по передаточной функции (16.3), которую необходимо представить в виде дробно-рациональной функции по степеням z-1 (см. лекцию 12):
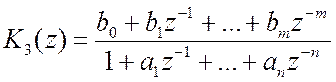 (16.6)
(16.6)
Используя для передаточной функции (16.4) представленное аналогичное (16.6), можно записать разностное уравнение для ошибки e[k], k=0,1,2,…
Контрольные вопросы
1. Дайте определение дискретной САУ. Какие системы относятся к дискретным САУ?
2. Дайте краткую характеристику математического аппарата дискретного преобразования Лапласа и Z-преобразования.
3. Какую функцию называют решетчатой?
4. Как записываются передаточные функции линейной дискретной системы?
5. Какой вид имеет обобщенная структурная схема дискретной следящей системы?
6. Как записывается разностное уравнение дискретной САУ?
ТЕМА 17: «ПОКАЗАТЕЛИ КАЧЕСТВА УПРАВЛЕНИЯ ДИСКРЕТНЫХ
СИСТЕМ РАДИОАВТОМАТИКИ»
Анализ устойчивости дискретных систем РА
Характеристическое уравнение дискретной замкнутой системы получается из передаточной функции (16.3) путем приравнивания ее знаменателя к нулю:
![]() (17.1)
(17.1)
Напомним, что необходимым и достаточным условием устойчивости непрерывной замкнутой системы является расположение корней характеристического уравнения на плоскости комплексной переменной р слева от мнимой оси (см. лекцию 6). Учитывая связь между переменными р и z=epT, требование к корням характеристического уравнения дискретной системы можно сформулировать так: замкнутая система устойчива, если все корни характеристического уравнения (17.1) расположены на плоскости комплексной переменной zвнутри круга единичного радиуса (рис.17.1,а).
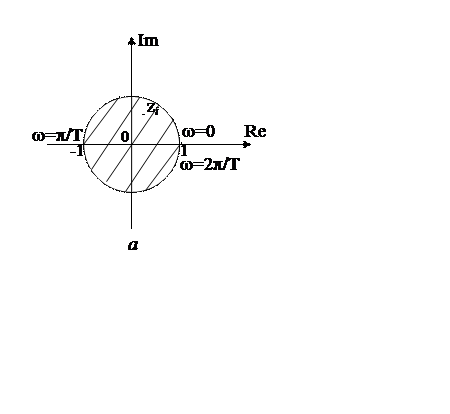

Рис.17.1
В силу периодичности функции epT указанное соответствие между допустимыми областями
для корней характеристического уравнения непрерывной и дискретной систем
ограничивается полосой частот от 0 до 2π/T(или ![]() )
– годограф вектора ejwTсовершает
один оборот (рис.17.1,а). Это не позволяет применить непосредственно ни
один из известных критериев устойчивости непрерывных систем. Отмеченную
трудность можно обойти, если ввести комплексную переменную
)
– годограф вектора ejwTсовершает
один оборот (рис.17.1,а). Это не позволяет применить непосредственно ни
один из известных критериев устойчивости непрерывных систем. Отмеченную
трудность можно обойти, если ввести комплексную переменную
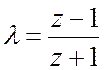 (17.2)
(17.2)
и так называемую псевдочастоту
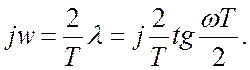 (17.3)
(17.3)
На
частотах ω<2/T псевдочастота w=ω.
При изменении частоты ω от ![]() псевдочастота
принимает значения от –∞ до ∞, а комплексная переменная
псевдочастота
принимает значения от –∞ до ∞, а комплексная переменная ![]() изменяется от
изменяется от ![]()
![]() , т.е. внутренняя часть круга
единичного радиуса (рис.17.1,а) отображается в левую полуплоскость комплексной
переменной
, т.е. внутренняя часть круга
единичного радиуса (рис.17.1,а) отображается в левую полуплоскость комплексной
переменной ![]() (рис.17.1,б). Следовательно,
для оценки расположения корней характеристического уравнения на плоскости
(рис.17.1,б). Следовательно,
для оценки расположения корней характеристического уравнения на плоскости ![]() могут быть использованы критерии
устойчивости, разработанные для непрерывных систем.
могут быть использованы критерии
устойчивости, разработанные для непрерывных систем.
В частности, при использовании критерия Гурвица необходимо перейти от характеристического уравнения (17.1) к уравнению
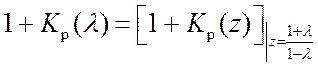
![]() .
.
Далее,
как и для непрерывной системы, составляется главный определитель Гурвица и
проверяются условия ![]() (см. лекцию 6).
(см. лекцию 6).
Устойчивость дискретных систем РА можно оценить и с использованием частотных критериев. Применение критерия Найквиста требует построения АФХ разомкнутой дискретной системы (годографа)
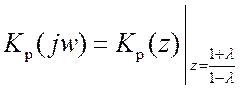 при
при
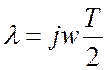 , (17.4)
, (17.4)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.