Частотные критерии являются графоаналитическими и обеспечивают наглядность инженерных расчётов. Они позволяют определить устойчивость замкнутой системы на основе экспериментально полученных частотных характеристик (АЧХ и ФЧХ) звеньев и разомкнутой системы в целом (т. е. в том случае, когда передаточные функции системы не известны).
В радиоавтоматике наибольшее применение находит критерий Найквиста, основанный на анализе амплитудно-фазовой частотной характеристики (АФХ) разомкнутой системы. Под АФХ понимают кривую на комплексной плоскости, представляющую геометрическое место конца вектора комплексного коэффициента передачи Kр(jw) при изменении частоты от нуля до бесконечности (данную кривую называют также годографом).
Условие устойчивости по критерию Найквиста формулируется следующим образом: замкнутая система устойчива, если АФХ разомкнутой системы для 0 £ w £ µ не охватывает точку с координатами (–1, j0).
Если система является астатической, т.е. содержит хотя бы одно интегрирующее звено, то для применимости критерия Найквиста необходимо дополнять АФХ дугой бесконечно большого радиуса и определять её расположение относительно точки (–1, j0). Критерий Найквиста при этом используется с учётом приведённой формулировки.
На рис. 9.2 приведены примеры АФХ устойчивых и неустойчивых статических (рис. 9.2, а) и астатических (рис. 9.2, б) систем.
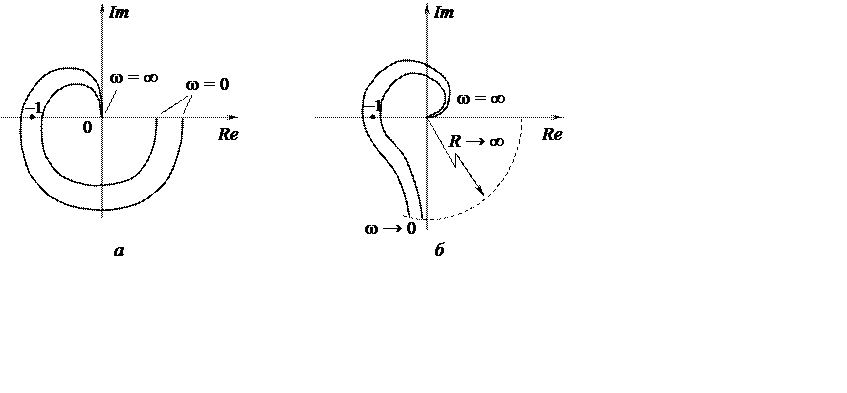
Рис. 9.2
Для исследования устойчивости замкнутых систем по
критерию Найквиста часто используют логарифмические частотные характеристики.
При этом следует учитывать, что точке АФХ с координатами (–1, j0)
соответствуют критические значения ЛАХ и ЛФХ 
дБ,
jкp = – p рад (рис. 9.3).
Рис. 9.3
Определение устойчивости систем для заданных параметров, а также выбор некоторых параметров должны производиться с учетом запаса устойчивости. Требуемый запас устойчивости системы определяется рядом причин: идеализацией звеньев автоматической системы; погрешностью определения параметров (коэффициентов усиления, сопротивлений, емкостей, постоянных времени и др.) в ходе расчета или экспериментального исследования; случайными разбросами и отклонениями параметров из-за различных дестабилизирующих факторов (например, изменения температуры) и прочее. Применительно к системам радиоавтоматики одним из основных факторов, определяющих устойчивость, является нестабильность амплитуды принимаемого сигнала из-за меняющихся условий распространения, дальности до подвижного объекта и других причин.
Определяя запас устойчивости, обычно вводят понятие о запасе устойчивости по фазе и по амплитуде (по усилению). Оба эти запаса рассматриваются одновременно.
Формулировка запаса устойчивости зависит от выбранного критерия. При использовании критерия Найквиста запас устойчивости тем больше, чем дальше расположена АФХ от критической точки (рис. 9.4, а).
Запасом по фазе
Dj называют угол, равный разности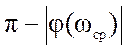 
.
Частота wср,
соответствующая вектору Kp(jwср), имеющему модуль, равный единице, называется частотой
среза разомкнутой системы.
Запас устойчивости по усилению DК определяется величиной отрезка оси абсцисс, заключенного между критической точкой (–1, j0) и АФХ.
При использовании логарифмических характеристик запас по фазе Dj находят по кривой ЛФХ при wср а запас по усилению DL – по кривой ЛАХ при j = – p рад (рис. 9.4, б).
Рис. 9.4
Для того, чтобы система обладала определённым запасом устойчивости, на графики ЛАХ и ЛФХ наносятся запретные области по заданным запасам DK и Dj. Эти области (рис. 9.5) представляют прямоугольники, ограниченные для ЛАХ горизонтальными линиями на расстоянии 201g (1+DK) и 201g (1 – DK) от оси абсцисс, а для ЛФХ – линиями (p – Dj) и (p+Dj). Считается, что система обладает запасом по усилению и по фазе, если частотные характеристики не заходят в запретные области (на рисунке заштрихованы).
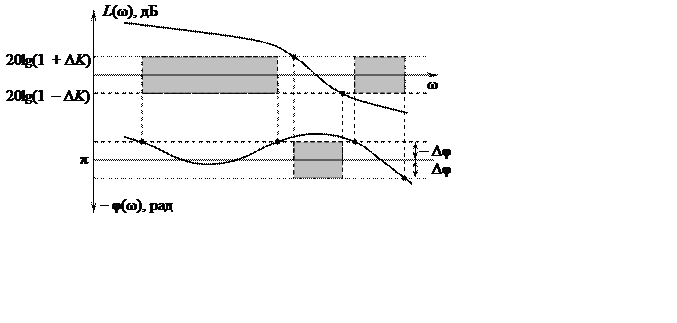
Рис. 9.5
Численные значения DL (или DK) и Dj, характеризующие запас устойчивости определяются обычно опытным путём для систем определённых классов. В радиоавтоматике принято считать достаточным запас по фазе Dj > p/6 рад и по усилению DL>6 дБ (или DK>0,5). Такой выбор позволяет обеспечить и заданный характер переходного процесса.
Контрольные вопросы
1. Как записывается характеристическое уравнение замкнутой системы?
2. Сформулируйте общие требования к устойчивости системы.
3. Поясните использование критерия Гурвица для анализа устойчивости систем.
4. Как определяется критический коэффициент усиления разомкнутой системы? В чём его смысл?
5. Как формулируется критерий устойчивости Найквиста?
6. Как определяется устойчивость замкнутой системы при использовании логарифмических частотных характеристик?
7. Чем объясняется необходимость обеспечения запаса устойчивости? Как определяется запас устойчивости по АФХ и логарифмическим частотным характеристикам?
8. Какие системы называются структурно неустойчивыми? (Приведите примеры).
ЛЕКЦИЯ 11. ТЕМА 10: «ОЦЕНКА КАЧЕСТВА АВТОМАТИЧЕСКИХ СИСТЕМ В ПЕРЕХОДНОМ РЕЖИМЕ»
Основные показатели качества САУ.
Прямые и косвенные методы оценки качества переходного процесса.
Типы переходных процессов.
Перерегулирование и быстродействие автоматических систем.
Метод цифрового моделирования непрерывных САУ.
Определение показателей качества переходного процесса по АЧХ замкнутой системы.
Оценка качества переходного процесса по ЛАХ разомкнутой системы.
Изменение режима работы АС происходит в результате прикладываемых к ней внешних воздействий. В следящих системах задающее воздействие представляет собой случайный процесс. При этом надо так выбрать параметры и структуру системы, чтобы это воздействие воспроизводилось с минимальной ошибкой.
При исследовании качества процесса управления обычно рассматривают некоторые типовые воздействия в виде детерминированных функций времени: единичной скачкообразной, линейной, квадратичной, импульсной, гармонической. Наиболее распространенным является воздействие в виде скачкообразной функции.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.