Радиоавтоматика: основы теории и принципы построения автоматических систем, страница 27

        Зависимость модуля вектора 1– K_з(jw) от частоты определяет АЧХ   |1– K_з(jw)| (рис. 12.4, а). Как видно из рисунка, она соответствует фильтру верхних частот, в отличие от АЧХ K_з(w), соответствующей ФНЧ (рис. 12.4, б). Это означает, что для снижения динамической ошибки необходимо увеличивать полосу пропускания системы (шумовую полосу F_ш). В то же время увеличение F_ш, влечет возрастание дисперсии шумовой ошибки (по линейному закону).

Следовательно, выбор полосы F_ш системы должен производиться с учетом противоречивых требований обеспечения малыми обеих составляющих ошибки одновременно. Нахождение оптимального значения F_ш, при котором результирующая ошибка минимальна, составляет важнейшую задачу при проектировании радиотехнических следящих систем.

Рис. 12.3

    

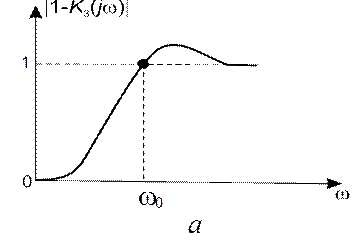
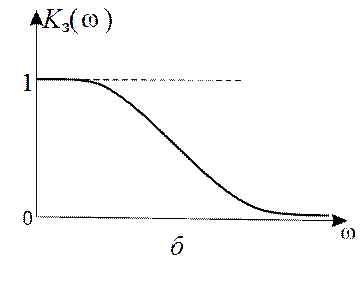
Рис. 12.4

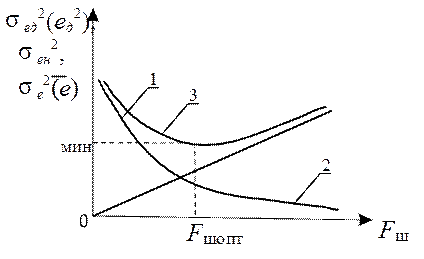
Рис. 12.5

Сказанное иллюстрируется рис. 12.5, на котором представлены зависимости: дисперсии динамической ошибки (или ее квадрата, если воздействие детерминированное) (кривая 1); дисперсии шумовой ошибки (прямая 2) и дисперсии (либо среднего квадрата) результирующей ошибки (кривая 3).

Контрольные вопросы

1. Как определяются характеристики эквивалентного шума, приведенного к входу дискриминатора?

2. Чем характеризуется точность следящих систем при воздействии помех?

3. Как определяется дисперсия шумовой ошибки? Какой смысл имеет шумовая полоса системы? Как она определяется?

4. Как определить дисперсию динамической случайной ошибки? В чем суть графического метода нахождения дисперсии ошибки?

ЛЕКЦИЯ 14. ТЕМА 13: «ОПТИМАЛЬНЫЕ ЛИНЕЙНЫЕ

ФИЛЬТРЫ СИСТЕМ РАДИОАВТОМАТИКИ»

План лекции

Критерий оптимизации следящей системы при детерминированном и случайном воздействиях.

Задача  параметрической оптимизации замкнутой АС.

Рассмотрим задачу оптимизации сглаживающего фильтра на примере системы слежения за задержкой сигнала (см. лекцию 4).Выбор структуры и параметров сглаживающего   фильтра, определяемых передаточной функцией , производится в соответствии с общими критериями, используемыми при синтезе оптимальных линейных следящих систем. Наиболее общим из них является критерий минимума среднеквадратической ошибки при заданной интегральной оценке переходного процесса:

                                        .             (13.1)

Здесь  − множитель Лагранжа;  − интегральная квадратичная динамическая ошибка, определяемая как

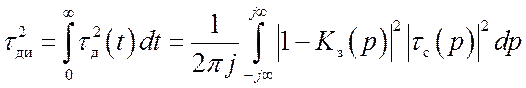                   ,                                                              (13.2)

где  − передаточная функция замкнутой системы,  − динамическая ошибка,  − изображение входного процесса ,  − оператор Лапласа.

В соответствии с (13.1) передаточная функция  оптимального следящего фильтра определяется из условия минимизации дисперсии  ошибки слежения при заданном значении . Поскольку требование конечной интегральной оценки  равносильно требованию нулевой динамической ошибки в установившемся режиме, то критерий (13.1) отвечает задаче минимизации  при заданной интегральной оценке переходного процесса и равенстве нулю динамической ошибки в установившемся режиме.

В силу специфики систем радиоавтоматики основным показателем качества для них является точность слежения в установившемся режиме при ограничении на время переходного процесса. К качеству переходного процесса предъявляются самые общие требования (допустимое перерегулирование). В связи с этим критерий оптимизации (13.1) может быть видоизменен: вместо интегральной квадратичной ошибки  используется динамическая ошибка в установившемся режиме 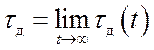 , которая весьма просто рассчитывается для типовых задающих воздействий.

Для полиноминальной модели  динамическая ошибка в установившемся режиме для системы n-го порядка астатизма определяется главным образом n-й производной от :, где ,  − параметр системы, зависящий от  (множителя Лагранжа), и определяемый как

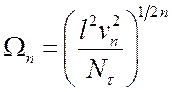                                            ,                 (13.3)

где  − спектральная плотность эквивалентных временных флуктуаций.

               Параметр  однозначно определяет передаточную функцию оптимального следящего фильтра. Так для линейной модели изменения задержки  оптимальным по критерию (13.1) является следящий фильтр с передаточной функцией

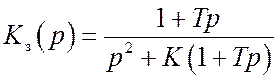                                     ,          (13.4)

соответствующей следящей системе с астатизмом 2-го порядка. Параметры системы  и  ( − добротность системы по ускорению) связаны с  соотношениями:  и . Передаточной функции (13.4) соответствует оптимальный фильтр с передаточной функцией  (астатический фильтр).

Шумовая полоса системы с передаточной функцией (13.4) равна

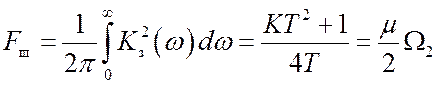                         ,                                                              (13.5)

где коэффициент .

Используя (13.5), находим параметр

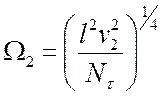                                             .                  (13.6)

Выразив через  (с использованием (13.6) дисперсию , а также квадрат динамической ошибки  в соответствии с (13.1) определяем значение

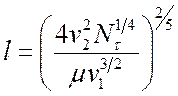                                            ,                 (13.7)

при котором достигается минимум среднего квадрата ошибки слежения в установившемся режиме для модели  с ускорением .

Оптимальные значения параметров системы определяются подстановкой (13.7) в (13.6) и использованием соотношений:

                               

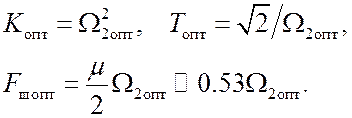
В отсутствие ускорения () критерием выбора шумовой полосы (и параметров ) является допустимое время установления синхронизации . Для линеаризованной системы с передаточной функцией (13.4) время переходного процесса можно оценить как . Следовательно, шумовая полоса может быть определена из условия обеспечения требуемого времени : , ограничивающего минимально достижимую дисперсию шумовой ошибки  (при нулевой динамической ошибке) в установившемся режиме.

Для удовлетворительного качества переходного процесса значение параметра  необходимо выбирать из условия , гарантирующего допустимое перерегулирование . При  переходной процесс апериодический (без перерегулирования).

Контрольные вопросы

1. Сформулируйте критерии оптимальности фильтра Винера–Колмогорова и фильтра Калмана.

2. Какой фильтр является оптимальным для линейной модели задающего воздействия?