Радиоавтоматика: основы теории и принципы построения автоматических систем, страница 7

Обратимся теперь к математическому описанию системы АПЧ. Полагаем, что все функциональные элементы, за исключением ФНЧ, являются безынерционными. Это предположение упростит математическое описание системы АПЧ, поскольку безынерционный элемент полностью описывается статической характеристикой – алгебраическим уравнением, связывающим входную и выходную переменные. Обоснованность такого допущения определяется тем, что полоса пропускания разомкнутой системы определяется, главным образом, фильтром нижних частот.

С учетом сказанного связь между частотами входного сигнала, гетеродина и сигнала промежуточной частоты определяется выражением

f_п=f_c – f_г                                                      (3.1)

(переменная t в (3.1) опущена, так как эти величины относятся к одному моменту времени). Отклонение промежуточной частоты от номинального значения (частотная расстройка) равна

Df=f_п – f₀.                                                                          (3.2)

Полагаем, что частотный дискриминатор точно настроен на частоту f₀, т.е. нуль дискриминационной характеристики соответствует этому значению частоты f_п. Учет дрейфа нуля дискриминационной характеристики (из-за дестабилизирующих факторов) сводится к добавлению в правой части (3.2) слагаемого Df_п (в общем случае случайная величина).

Напряжение на выходе дискриминатора представим в виде

U_д(t)=U(Df)+n(t, Df),                                        (3.3)

где составляющая U(Df) является полезной (обусловлена действием сигнала), а составляющая n(t,Df) описывает помеху, действующую на выходе дискриминатора (характеристики ее в общем случае зависят от частотной расстройки).

Управляющее напряжение формируется фильтром нижних частот, описываемым дифференциальным уравнением:

U_у(t)=K_ф(p)U_д(t),                                (3.4)

где К_ф(р) – передаточная функция ФНЧ. Вид передаточной функции К_ф(р) определяет важнейшие характеристики системы АПЧ: запас устойчивости, быстродействие, полосу захвата, точность.

В случае применения системы АПЧ для стабилизации промежуточной частоты применяется, как правило, простейший RC-фильтр нижних частот (инерционное звено), постоянная времени которого выбирается таким образом, чтобы ФНЧ не пропускал составляющих напряжения U_д(t), обусловленных модуляцией сигнала (АМ, ЧМ) и в то же время передавал без искажений составляющую, обусловленную уходом частоты генераторов (передатчика и гетеродина) вследствие нестабильности, а также из-за эффекта Доплера.

В следящих фильтрах, используемых в доплеровских измерителях скорости, применяются более сложные ФНЧ, содержащие несколько интегрирующих звеньев, а также другие типовые звенья. Это необходимо для того, чтобы уменьшить динамическую ошибку, обусловленную инерционностью системы.

Регулировочная характеристика f_г(U_y) подстраиваемого генератора в общем случае нелинейная (рис. 3.3). Однако при небольших частотных расстройках она достаточно точно аппроксимируется линейной зависимостью:

,                                                          (3.5)

где 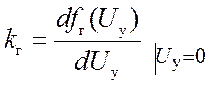– крутизна регулировочной характеристики (коэффициент передачи подстраиваемого генератора, имеющий размерность Гц/В). Максимальное значение U_ymax управляющего напряжения определяет полосу удержания 2Df_y системы – диапазон частотных расстроек, которые могут быть скомпенсированы системой при условии, что она работает в режиме слежения (частотная ошибка близка к нулю). Полоса удержания системы АПЧ всегда больше, чем полоса захвата, под которой понимается диапазон частотных расстроек, при которых возможно установление режима слежения (строгое определение полосы захвата возможно лишь с использованием нелинейной теории систем АПЧ и будет дано позже).

Структурная схема системы АПЧ, построенная на основе уравнений (3.1) – (3.5), имеет вид:

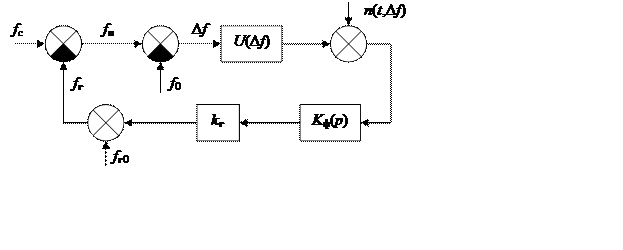
Рис. 3.4

Первые два уравнения реализуются на модели элементами сравнения, уравнение (3.3) моделируется безынерционным нелинейным звеном с характеристикой U(Df) и сумматором. Уравнение (3.4) соответствует линейному звену с передаточной функцией К_ф(р). Последнее уравнение моделируется совокупностью линейного безынерционного звена с коэффициентом передачи k_г и сумматора. Учет нестабильности частоты Df_г подстраиваемого генератора и дрейфа нуля дискриминационной характеристики Df_п производится добавлением их к величинам f_г0 и f₀ соответственно.

Можно упростить структурную схему, если под входной и выходной переменными понимать не сами частоты f_c и f_г, а их отклонения от номинальных значений:

Df_c=f_c – f_c0  и  Df_г=f_г – f_г0

Это позволяет объединить два элемента сравнения, так как

Df_c – Df_г=(f_c – f_c0) – (f_г – f_г0)=(f_c – f_г) – (f_c0 – f_г0)=f_п – f₀=Df.          (3.6)

Дальнейшего упрощения структурной схемы можно достичь, если полагать, что частотная расстройка мала (Df®0). Такое допущение справедливо для работы системы в режиме слежения. Тогда дискриминационная характеристика может быть аппроксимирована линейной зависимостью

U(Df)=k_дDf,                                                (3.7)

где 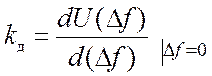 – крутизна характеристики (коэффициент передачи частотного дискриминатора, имеющий размерность В/Гц).

С учетом (3.6) и (3.7) структурная схема системы АПЧ принимает вид (рис. 3.5).

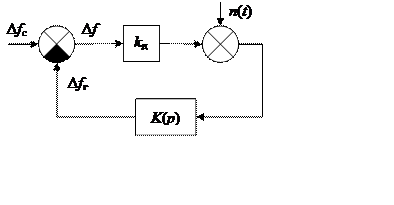
Рис. 3.5

Передаточная функция К(р)=k_гК_ф(р) описывает ФНЧ и подстраиваемый генератор. Данная схема соответствует линейной системе, описываемой линейным дифференциальным уравнением:

Df_г=k_гК_ф(р)[k_д(Df_c – Df_г)+n(t)]                             (3.8)

(переменная t у величин Df_c и Df_г опущена в целях простоты записи).

Структурная схема (рис. 3.5) и уравнение (3.8) могут быть использованы для решения таких задач, как определение устойчивости, быстродействия, точности слежения в установившемся режиме. Однако для определения такой важной характеристики, как полоса захвата, линейная модель системы непригодна, так как не учитывает нелинейности характеристики дискриминатора.

Контрольные вопросы

1. Укажите области применения систем АПЧ.