Радиоавтоматика: основы теории и принципы построения автоматических систем, страница 21

7. Сформулируйте правила переноса узла суммирования и точки разветвления через звено.

8. Напишите выражения для основных передаточных функций замкнутой системы. Поясните, как они получены.

9. Поясните фильтрующую способность следящей системы. Изобразите АЧХ замкнутой системы.

10. Чем обусловлена динамическая ошибка следящей системы? Как влияет форма АЧХ замкнутой системы на величину динамической ошибки?

ЛЕКЦИЯ 9. ТЕМА 9: «УСТОЙЧИВОСТЬ АВТОМАТИЧЕСКИХ

 СИСТЕМ»

План лекции

Общие требования к устойчивости автоматических систем.

Алгебраические критерии устойчивости.

9. 1. Общие требования к устойчивости систем

Основным показателем качества АС является ее устойчивость. Устойчивость линейных систем не зависит от величины возмущения; система, устойчивая при малых возмущениях, будет устойчивой и при больших возмущениях. При этом судить об устойчивости можно по корням характеристического уравнения замкнутой системы:

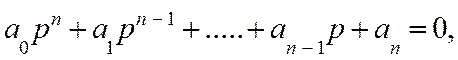                          (9.1)

которое составляется на основании однородного дифференциального уравнения, описывающего свободное движение системы (т. е. в отсутствие возмущения):

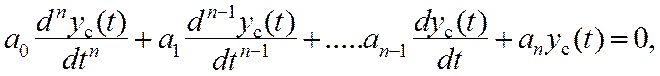                 (9.2)

где а₀, а₁, …, а_n – постоянные коэффициенты, определяемые параметрами системы; y_c(t) – составляющая выходной переменной, определяющая свободное движение системы.

Известно, что при отрицательных вещественных корнях уравнения (9.2), составляющая свободного движения при t® µ монотонно убывает до нуля (рис. 9.1, а). Для пары комплексных корней с отрицательной вещественной частью составляющая свободного движения при t®µ также убывает до нуля по закону затухающего колебания (рис. 9.1, б).

Рис. 9.1

Аналитические выражения составляющих свободного движения имеют вид

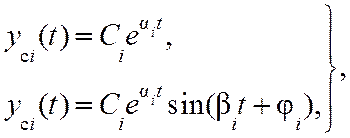                                 (9.3)

где С_i – постоянные интегрирования, определяемые из начальных условий; a_i – вещественная часть корня (интенсивность затухания колебаний); b_i – мнимая часть корня (частота собственных колебаний); j_i  – начальная фаза.

Система устойчива при отрицательных корнях и отрицательных вещественных частях корней. В случае положительного вещественного корня составляющая свободного движения при t®µ неограниченно возрастает      (рис. 9.1, в). Для пары комплексных корней с положительной вещественной частью составляющая свободного движения при t®µ также возрастает по закону расходящегося колебания (рис. 9.1, г).

Если среди корней характеристического уравнения есть хотя бы одна пара чисто мнимых, то появится составляющая свободного движения в виде незатухающего колебательного процесса (система находится на границе устойчивости и неустойчивости). Таким образом, необходимым и достаточным условием устойчивости системы является соблюдение того, чтобы все корни лежали в левой полуплоскости (рис. 9.2).

При этом можно не вычислять корни характеристического уравнения, надо лишь выяснить, все ли корни расположены слева от мнимой оси.

Математическая формулировка условий, которым должны удовлетворять коэффициенты характеристического уравнения или какие - либо функции этих коэффициентов, чтобы система была устойчивой, называется критерием устойчивости. Критерии устойчивости делят на алгебраические и частотные. Они позволяют выяснить, все ли корни характеристического уравнения замкнутой системы находятся в левой полуплоскости без решения этого уравнения.

Рис. 9.1

9.2. Алгебраические критерии устойчивости

Алгебраические критерии устойчивости позволяют по коэффициентам характеристического уравнения замкнутой системы определить, все ли корни находятся в левой полуплоскости, не решая этого уравнения. Наибольшее применение в радиоавтоматике находит критерий Гурвица, который формулируется с использованием определителей. При этом определители Гурвица составляются по коэффициентам характеристического уравнения (9.4). Используя коэффициенты этого уравнения, составляют главный определитель Гурвица. Для этого все коэффициенты, начиная с коэффициента при (n–1)-й производной, выписывают последовательно до свободного члена по главной диагонали. Столбцы вверх от главной диагонали дополняют коэффициентами с убывающими индексами. Места, которые должны быть заняты коэффициентами с индексом выше n и ниже 0, заполняют нулями.

Для уравнения n-й степени главный определитель Гурвица

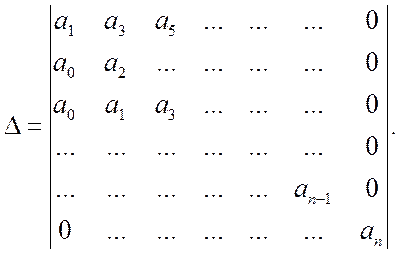                         (9.4)

        Для того, чтобы характеристическое уравнение (9.1) имело все корни с отрицательной частью, главный определитель (9.4), а также все его диагональные миноры D₁, D₂, … должны быть положительными. Номер диагонального минора определяется номером коэффициента по диагонали, до которого составляется данный минор:

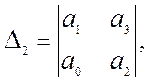
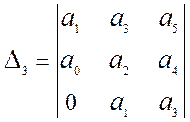         и т. д.                 (9.5)

Последний столбец главного определителя содержит только один коэффициент a_n , отличный от нуля, поэтому

.

Для положительных коэффициентов уравнения (необходимое условие устойчивости) a_n > 0, следовательно, D_n > 0, если D_{n – 1} > 0. Таким образом, следует вычислять миноры D₂, D₃, …, D_{n – 1} .

Если все миноры, кроме предпоследнего, положительны, а минор D_{n – 1} равен нулю, то система находится на границе устойчивости. Полагая все параметры системы, кроме одного (обычно это общее усиление системы), известными, можно определить критическое значение этого параметра, при котором система находится на границе устойчивости.

Поскольку характеристическое уравнение замкнутой системы определяется знаменателем передаточной функции, а все передаточные функции (независимо от входа и выхода) имеют один и тот же знаменатель (см. п. 8.3), то при анализе устойчивости системы используют ту передаточную функцию, которая имеет наиболее простой вид (простой числитель).

ЛЕКЦИЯ 10. ТЕМА 9: «УСТОЙЧИВОСТЬ АВТОМАТИЧЕСКИХ

 СИСТЕМ»

(продолжение)

План лекции

Частотные критерии устойчивости.

Запас устойчивости.

9.3. Частотные критерии устойчивости

Частотные критерии позволяют судить об устойчивости замкнутых АС по частотным характеристикам условно разомкнутых систем без определения корней характеристического уравнения замкнутой системы.