Радиоавтоматика: основы теории и принципы построения автоматических систем, страница 30

Поскольку порядок уравнений (15.4) n=1, то необходимым и достаточным условием устойчивости является положительность коэффициентов (см. лекцию 7). Коэффициент >0 всегда (Т имеет смысл постоянной времени), а коэффициент

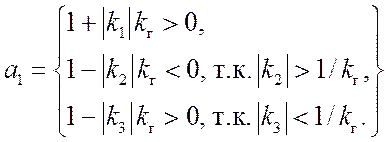                                                                    (15.5)

Знак при втором слагаемом каждого из трех равенств определяется значением аргумента φ_i: φ₁=0, φ₂= π, φ₃= π.

Таким образом, точки А и С являются точками устойчивого равновесия (система устойчива «в малом»), а точка В соответствует неустойчивой системе.

В третьем случае (рис.15.2,в) частотная расстройка такова, что существует лишь одна точка С устойчивого равновесия, расположенная за пределами раскрыва ДХ. Это означает, что захват по частоте при такой расстройке невозможен (система разомкнута).

На рис.15.3,а приведены графики ДХ и «обратной» регулировочной характеристики ПГ – прямой линии с наклоном –1/k_г, соответствующие предельно допустимому значению частотной расстройки. Прямая 1 соответствует значению  а прямая 2 – значению определяющим соответственно полосу захвата и полосу удержания системы АПЧ. Каждая из указанных прямых является касательной по отношению к ДХ: прямая 1 – в области «нижнего» изгиба, а прямая 2 – в точке, соответствующей пиковому значению ДХ. При симметричной ДХ (нечетная симметрия) указанные полосы определяют возможности захвата и слежения без срыва при расстройке Δf  любого знака.

	U(Δf)
			Δf0

 

2Δfзхв

0

б

Δfс

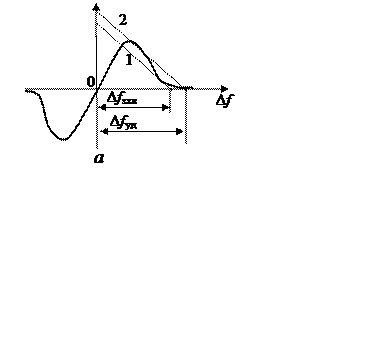
Рис.15.3

 Зависимость остаточной  частотной ошибки (статической ошибки) f₀от начальной расстройки Δf_с, построенная с использованием описанного графо- аналитического метода, представлена на рис.15.3,б (стрелками показано направление изменения расстройки Δf_с). В режиме слежения увеличение частотной расстройки от 0 до Δf_уд сопровождается сравнительно медленным ростом статической ошибки. При Δf_с= Δf_уд происходит срыв слежения: ошибка резко возрастает до значения, практически равного Δf_с (система размыкается). В режиме захвата система остается разомкнутой при уменьшении частотной расстройки вплоть до значения Δf_с= Δf_зхв (точки В и С на рис.15.2,б сближаются до полного совпадения в момент захвата). При этом существует единственное решение (точка А на рис.15.2,а) уравнения 15.2: статическая ошибка резко уменьшается и система переходит в режим слежения.

Полоса удержания системы АПЧ связана с параметрами ЧД и подстраиваемого генератора соотношением Δf_уд=U_maxk_г(см. лекцию 3), а полоса захвата всегда меньше , чем Δf_уд. Увеличение полосы удержания влечет и увеличение полосы захвата, которая наряду с точностью является важнейшей характеристикой системы АПЧ (как и любой другой следящей системы).

Контрольные вопросы

1. Дайте определение нелинейной САУ.

2. Укажите основные методы анализа нелинейных САУ.

3. В чем заключается суть метода фазовой плоскости?

          4. Дайте кратную характеристику методов: кусочно-линейной аппроксимации, гармонической линеаризации, статистической линеаризации.

5. Чем обусловлены нелинейные режимы работы радиотехнических следящих систем?

6. В чем суть понятий «захват» сигнала и «срыв слежения»?

7. Изобразите обобщенную структурную схему нелинейной следящей системы.

8. Запишите нелинейное уравнение для системы АПЧ в установившемся режиме.

9. Поясните сущность графоаналитического метода анализа нелинейной системы АПЧ.

10. Дайте определение полосы захвата и полосы удержания системы АПЧ.

11. Как определить полосу захвата и полосу удержания системы АПЧ графическим методом?

ЛЕКЦИЯ 16.  ТЕМА16: «АНАЛИЗ ДИСКРЕТНЫХ СИСТЕМ

РАДИОАВТОМАТИКИ»

План лекции

Обобщенная структурная схема дискретной следящей системы.

Передаточные функции линейной дискретной системы.

Разностное уравнение дискретной системы РА.

Дискретные системы РА – это такие системы, в которых сигналы подвергаются дискретизации во времени (импульсные системы), по уровню (системы «релейного» типа) или во времени и по уровню (цифровые системы). Примером импульсной системы РА является система слежения за задержкой сигнала импульсной РЛС (см. лекцию 5). Наибольший практический интерес представляют цифровые системы РА, обладающие по сравнения с аналоговыми системами (непрерывными и импульсными) рядом преимуществ: высокой стабильностью их параметров (отсутствуют аппаратурные погрешности ­­– дрейф «нуля» дискриминаторов и пр.), простотой перестройки их структуры (например, сглаживающих фильтров) и регулировки параметров, возможностью реализации оптимальных или близких к ним алгоритмов слежения за параметрами сигналов и др.

При реализации цифровых систем РА используются три возможных подхода: аппаратный, программный и комбинированный (аппаратно-программный). В первом случае используются цифровые устройства, реализуемые в основном на микросхемах малой и средней степени интеграции. Такие системы отличаются высоким быстродействием, однако их использование сопряжено с трудоемкой разработкой индивидуальной структуры. При программном подходе цифровые системы РА реализуются в виде программ для универсальной ЭВМ. Третий подход предусматривает разработку как аппаратурных, так программных средств главным образом на основе микропроцессорных устройств, к которым относятся собственно микропроцессоры или микропроцессорные комплекты (МПК) больших интегральных схем (БИС), а также различного рода микро-ЭВМ.

Основное направление в совершенствовании цифровых систем РА связано с использованием последних достижений  микроэлектроники для цифровой реализации систем РА. Если на ранних стадиях развития цифровых систем РА использовалось преимущественно бинарное (двухуровневое) квантование сигналов, а их реализация осуществлялась на аппаратном уровне, то в современных цифровых системах РА большинство задач по реализации алгоритмов управления возлагается на МПК или микро-ЭВМ (реализация алгоритмов преимущественно программным способом).