Радиоавтоматика: основы теории и принципы построения автоматических систем, страница 32

а сам критерий формулируется следующим образом: дискретная система, устойчивая в разомкнутом состоянии, устойчива и в замкнутом состоянии, если годограф АФХ не охватывает точку (–1,j0).

Запас устойчивости по фазе и по усилению определяется так же, как для непрерывных систем (формулы 17.4) при подстановке в них значений частоты ω_срсреза и критической частоты ω_кр, определенных по АФХ дискретной системы (на интервале ).

Анализ качества переходного процесса дискретных систем РА

  Одним из наиболее универсальных методов оценки качества переходного процесса в дискретной АС является метод, основанный на использовании разностного уравнения (16.5). Другая форма разностного уравнения дискретной АС относительно ошибки слежения имеет вид

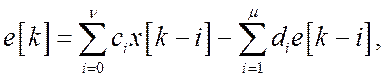                                                                    (17.5)

где с_iи d_i–коэффициенты, определяемые по передаточной функции

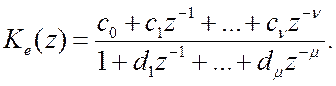
При заданном воздействии x(t) рекуррентные формулы (16.5), (17.5) позволяют рассчитать и построить графики дискретных переходных процессов y(kT) и e(kT), а по ним определить качественные показатели (быстродействие, перерегулирование и пр.– см. лекцию 8).

Анализ точности дискретной АС при детерминированном воздействии

   Ошибка слежения в дискретной системе РА в установившемся режиме при полиномиальной модели задающего воздействия определяется как

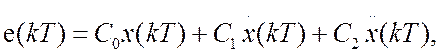                                                             (17.6)

где С₀, С₁ и С₂–коэффициенты ошибок по положению, по скорости и по ускорению соответственно (полиномиальная модель 2-го порядка), 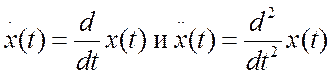– соответственно скорость изменения воздействия и ускорение.

   Коэффициенты ошибок определяют по формуле:

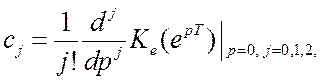
 или по более удобным для приложений формулам

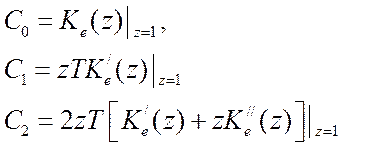
где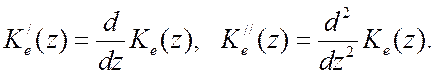  

В астатических системах 1-го и 2-го порядков астатизма коэффициенты ошибок С₀=0 и С₀=С₁=0 соответственно (статическая ошибка–ошибка по положению равна нулю). В системе 2-го порядка ошибка по скорости также равна нулю.

Анализ точности дискретной АС при воздействии помех

Точность дискретных АС при воздействии помех оценивают результирующей средней квадратической ошибкой

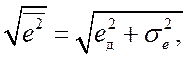
где e_д– математическое ожидание (динамическая ошибка, вычисляемая по формуле (17.6)), – дисперсия ошибки, обусловленной действием помехи.  

Дисперсия шумовой составляющей ошибки

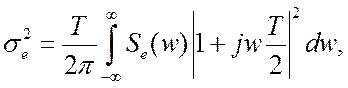
гдеS_e(w) – спектральная плотность ошибки, w – псевдочастота, определяемая выражением (17.3).

Анализ дискретных систем часто проводят с использованием приближенного метода, основанного на замене дискретной системы эквивалентной непрерывной ( квазинепрерывный метод). Данная замена справедлива, если частота дискретизации F_д=1/T удовлетворяет условиям , где F_x – эффективная ширина спектра воздействия x(t),   F_ш – шумовая полоса (одного порядка со значением F_x ). В этом случае анализ проводится с использованием математического аппарата теории линейных непрерывных систем (см. лекции 6–12).

Контрольные вопросы

1. Сформулируйте требования к корням характеристического уравнения устойчивой дискретной САУ.

2. Что называется псевдочастотой? Как она вводится? С какой целью она используется?

3. Поясните особенности применения алгебраического критерия Гурвица для анализа устойчивости дискретных САУ?

4. В чем заключается отличие применения частотного критерия Найквиста для анализа устойчивости дискретных САУ по сравнению с непрерывными системами?

5. Как оценить качество переходного процесса в дискретной САУ?

6. Как найти ошибку слежения дискретной САУ в установившемся режиме при типовых воздействиях: постоянном (скачкообразном), линейном, квадратичном?

ЛЕКЦИЯ 17. ТЕМА 18: «ЦИФРОВЫЕ СИСТЕМЫ

РАДИОАВТОМАТИКИ»

План лекции

Цифровые САУ. Преимущества цифровых САУ перед аналоговыми системами.

Функциональная схема цифровой следящей системы.

 Передаточные функции цифровой следящей системы.

Квазинепрерывный метод анализа цифровых САУ.

Линейная модель цифровой  САУ.

Несмотря на большое разнообразие цифровых систем РА, для описания любой цифровой следящей системы может быть использована обобщенная функциональная схема, представленная на рис.18.1,а.

а

       

 

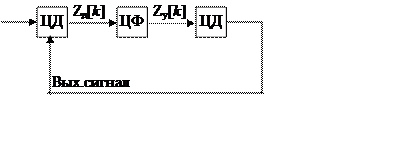
б

Рис.18.1

Цифровой дискриминатор (ЦД) предназначен для формирования сигнала ошибки , зависящего от ошибки слежения  Здесь k–порядковый номер сигнала ошибки (k=0,1,2,…), t=t_k–моменты дискретизации задающего воздействия и управляемой переменной.

Аналого-цифровое преобразование может производиться до, одновременно или после формирования сигнала ошибки. На рис.18.1 аналого­-цифровой преобразователь (АЦП) включен в блок «цифровой дискриминатор» (АЦП в контуре регулирования). Цифровой фильтр (ЦФ) преобразует цифровой сигнал ошибки  в цифровой управляющий сигнал , который в свою очередь преобразуется в аналоговый или цифровой выходной сигнал с помощью цифрового синтезатора (ЦС).

Цифровые системы РА представляют собой сложные нелинейные дискретные системы автоматического управления. Исследование их с использованием строгих методов анализа дискретных систем (см. лекцию 16) даже с учетом возможности их «линеаризации» представляет весьма сложную задачу. Для практических приложений представляет интерес так называемый  квазинепрерывный метод анализа цифровых систем, в котором ценой отказа от описания «несущественных» особенностей удается сравнительно просто описать и исследовать наиболее «существенные» особенности цифровой системы.

Квазинепрерывный метод применим к дискретным системам, которые могут быть приближенно представлены в виде последовательно соединенных нелинейной малоинерционной части (дискриминатор) и линейной части –линейные сглаживающие цепи (рис.18.1,б). Условием применимости квазинепрерывного метода является F_ш<<F_с, где F_ш–шумовая (или эквивалентная) полоса дискретной системы, F_с– полоса пропускания предшествующего тракта, определяемая шириной спектра сигнала (одного порядка или меньше, чем частота F_д дискретизации). Сущность метода сводится к учету дискретного характера преобразований лишь в нелинейной части. «Строгие» методы анализа учитывают дискретный характер преобразований в обеих частях (нелинейной и линейной), что становится необходимым при F_ш≈ F_с ≈ F_д (величины одного порядка). Классический метод сведения дискретной системы к непрерывной применим при F_ш<< F_диF_с<<F_д и основан на пренебрежении дискретным характером преобразований как в нелинейной, так и в линейной частях.